Repita o problema 36 para o circuito da Figura 10.97
- Itens do problema 36:
a) Determine as expressões matemáticas para o comportamento transitório da tensão e da corrente depois que a chave é fechada.
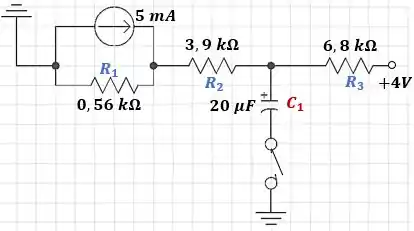
Passo 1
Olá galerinha! Antes de saírem correndo dessa questão, respirem…

Questões com essa, precisam de muita paciência, mas vamos no nosso ritmo de sempre.
Vamos anotar as informações do problema:
Passo 2
Esse tipo de problema, exige que façamos uma redução desse circuito, para um circuito mais simples de ser trabalhado.
Como primeira análise, vamos calcular a tensão fornecida pelo lado esquerdo do circuito:
Para isso só precisamos da primeira lei Ohm:
Passo 3
Agora vamos calcular a resistência equivalente () entre os resistores 1 e 2, que estão em série neste circuito:
Passo 4
Agora podemos reestruturar esse circuito:
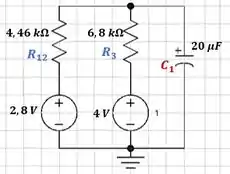
O circuito acima é equivalente ao circuito apresentado pela questão, para visualizar isso, basta comparar as relações em série e paralelo descritas no circuito original com as estabelecidas aqui.
Passo 5
Ainda podemos fazer mais uma redução, pois temos dois resistores ainda em paralelo. Então vamos calcular a resistência equivalente dessa ligação. Para ligações em paralelo, temos a relação:
Reorganizando essa equação, temos:
Atribuindo os valores:
Passo 6
Análogo ao processo para os resistores, temos que reduzir as fontes de tensão a uma única, para isso temos o teorema de Thévenin. Mas como passo anterior a esse, é preciso conhecer a corrente, pois é necessária para determinação da tensão. Para isso, usaremos a lei de Ohm para malha da esquerda.
Agora temos todas as informações para calcular a tensão:
Passo 7
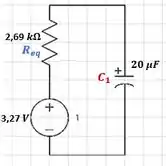 Agora podemos reestruturar o circuito:
Agora podemos reestruturar o circuito:
Assim, a determinação da das equações se torna simples 😋, pois a constante de tempo será expressar por:
Passo 8
As equações matemáticas e serão escritas como:
e,
Passo 9
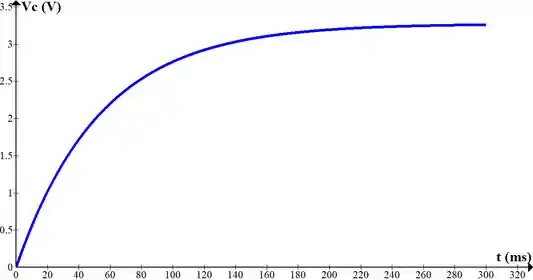
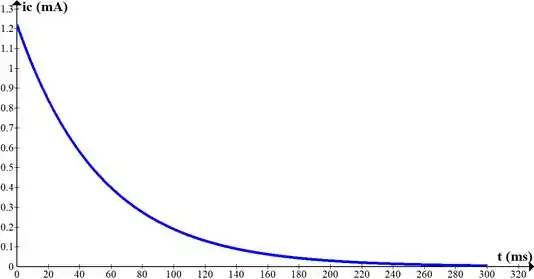
Resposta
a) ;