Repita o Problema 10 para o circuito ilustrado na figura 5.81
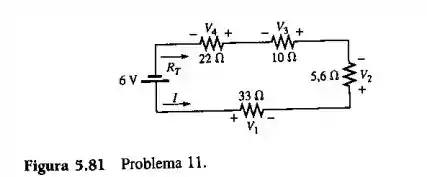
Passo 1
E ai meus amores, tudo bem?
Borá?
- Como as resistências estão conectadas em série,
- Aplicaremos a lei das tensões de Kirchhoff
- Considerando a fórmula , iremos encontrar a potência total fornecida ao circuito
- Use a fórmula e encontre a potência mínima de cada resistor.
Aplicaremos a lei de Ohm ao circuito e iremos calcular a corrente.
Passo 2
Iremos aplicar Ohms e determinar o valor de
Iremos aplicar Ohms e determinar o valor de
Iremos aplicar Ohms e determinar o valor de
Iremos aplicar Ohms e determinar o valor de
Portanto, o valor de são respectivamente .
Passo 3
Vamos substituir , e provar a lei das tensões
Portanto, a lei das tensões de Kirchhoff é verificada!
Passo 4
Usando a fórmula iremos encontrar a potência dissipada no resistor de .
Usando a fórmula a seguir iremos encontrar a potência dissipada no resistor de .
Passo 5
Usando a fórmula a seguir iremos encontrar a potência dissipada no resistor de .
Usando a fórmula a seguir iremos encontrar a potência dissipada no resistor de .
Verificando se a potência total fornecia é igual a potência dissipada nos resistores
Portanto, o valor da potência dissipada nos resistores é , a potência total fornecida é de . Onde, a potência total fornecida é igual à potência dissipada nos resistores.
Passo 6
Aqui, para todos os resistores, a potência nominal é inferior a 0,5 W. As potências do resistor de 1 W e 2 W são muito grandes para os valores de potência obtidos.
Portando, a potência mínima dos resistores que pode ser usados é de 1/2 W.
Resposta
- Portanto, o valor de são respectivamente .
- Portanto, a lei das tensões de Kirchhoff é verificada!
- Portanto, o valor da potência dissipada nos resistores é , a potência total fornecida é de . Onde, a potência total fornecida é igual à potência dissipada nos resistores.
- Portando, a potência mínima dos resistores que pode ser usados é de 1/2 W.