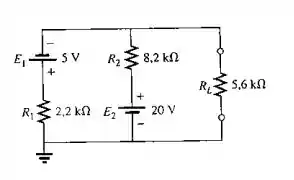
Repita o Problema 26 para o circuito mostrado na Figura 9.141.
Passo 1
Falaaaaaa pessoal, show de bola??
Bora resolver esse exercício na maciotaaaaa, então siimboraa!!
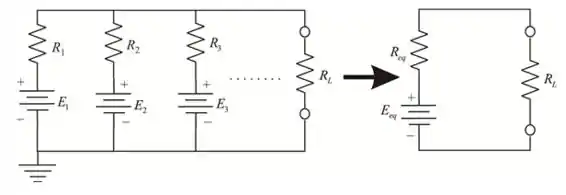
Através da aplicação do teorema de Millman, qualquer número de fontes de tensão paralelas pode ser reduzido a um.
Passo 2
A resistência equivalente é dada por
E
Passo 3
Para o circuito dado, a tensão equivalente é
A resistência equivalente é
Assim, a resistência equivalente é .
Passo 4
O circuito de Millman equivalente é
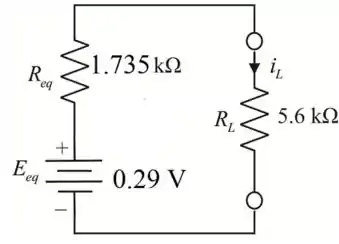
A corrente no resistor é dada por
Assim, a corrente no resistor é
A tensão no resistor é
Portanto, a tensão no resistor é
Resposta
Assim, a resistência equivalente é.
Assim, a corrente no resistor é
Portanto, a tensão no resistor é