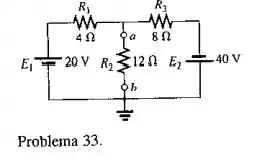
Repita o Problema 31 para o circuito mostrado na Figura 9.147. Faça o com cuidado!
Passo 1
Boraaa galerinha, aniimaaa, vamos resolver mais um!!
Só bora então!!
Se o circuito dado for modificado parar o circuito equivalente de Millman, é muito conveniente resolver o problema dado pelo teorema de substituição.
Portanto, usando o teorema de Millman, o circuito dado pode ser modificado para uma única fonte de tensão em série com uma resistência
Passo 2
O valor de é dado
O VALOR DE é
Uma vez em que nenhum fluxo de corrente e nenhuma queda de tensão ocorrerá em .
Portanto ,
Passo 3
Os três ramos equivalentes são dados por
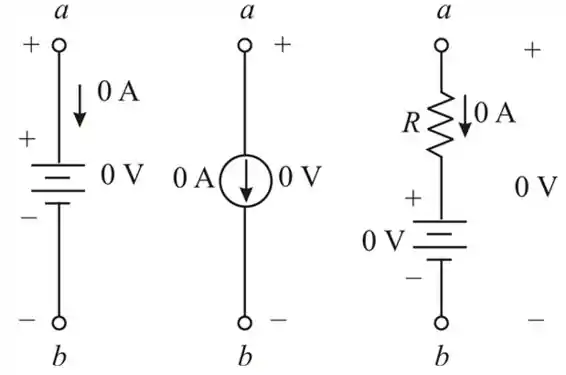
Resposta
Vide a figura do passo 3!