Repita o Problema 10 para o circuito visto na Figura 15.123
Passo 1
Faaaala galera do responde aí
precisamos calcular a impedância total
E no final vamos deixar nesse formato
substituindo os valores
o ângulo pode ser obtido dessa forma
e assim temos nossa resposta
Passo 2

Passo 3
Para encontrar vou usar a seguinte definição
Então a gente isolar a incógnita
Para resolver este item a gente vai precisar dessa equação
Vamos isolar a variável
com os dados da figura podemos substituir
Passo 4
item (d)
Substituindo
e para o ângulo
agora iremos determinar
observação, aqui somaremos o ângulo ( ao contrário de quando determinamos )
e para determinar faremos assim
Passo 5
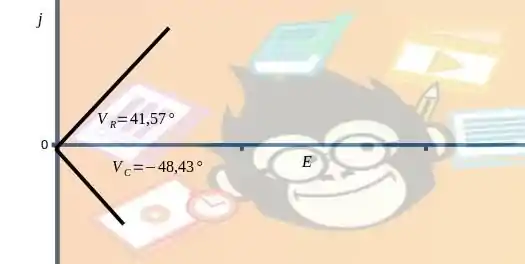
Passo 6
Vamos verificar a seguinte igualdade
Primeiro usaremos algumas propriedades anteriores
mais um detalhe
Belezinha até aqui?
Lembra que calculamos como ?
bora substituir de novo
simplificando
a igualdade é verdadeira
Caso substituíssemos os números, o valor também seria verdadeiro, porque usamos essas definições na hora de calcular os valores
Passo 7
A fórmula para potência média é
substituindo
tranquilo, né?
Passo 8
O fator de potência será
Passo 9
Para finalizar vamos escrever as expressões senoidais
Esses são os valores que já calculamos
Passo 10
As formas de ondas serão baseadas nas equações do Passo 9, olhe a Figura 15.39, a diferença é que será usado os valores do passo anterior.
Resposta
a.
b. Resposta no passo 2
c.
d.
e. Resposta no Passo 5
f. Resposta no passo 6
g.
h.
i.
j. Resposta no Passo 10