Repita o problema 22 para o circuito visto na Figura 20.62.
a. Calcule o valor de para a ressonância.
b. Calcule .
c. Calcule a frequência de ressonância () se a largura de banda for 1 kHz.
d. Calcule o valor máximo da tensão .
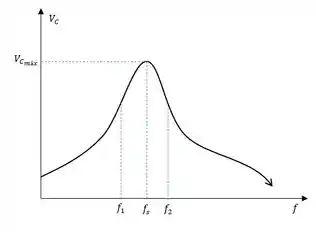
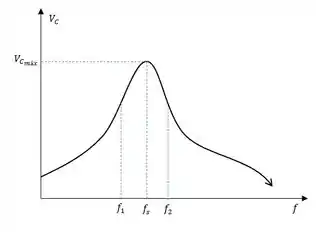
e. Plote a curva de em função da frequência. Indique o valor máximo, a frequência de ressonância e as frequências de corte.
Passo 1
Fala galerinhaaaa, tudo certo? Bora bora resolver mais uma questão??
Ao observarmos o circuito, temos que pode ser obtido pela seguinte relação:
Passo 2
Já para calcularmos , basta aplicarmos a fórmula:
Passo 3
Para calcularmos o valor da frequência de ressonância, devemos primeiro encontrar :
Agora podemos calcular a frequência através da fórmula de largura de banda (BW):
Passo 4
O valor máximo de pode ser dado por:
Passo 5
Prontinho, finalizamos essa!!!! Partiu resolver mais uma?
Resposta
a.
b. .
c. .
d. .
e. e