Repita o problema 17 para R=1 M e compare os resultados.
a) Determine a constante de tempo do circuito.
b)Escreva a equação matemáica para a tensão Vc depois que a chave é fechada.
c)Determine a tensão Vc depois de transcorrida uma, três e cinco constantes de tempo.
d)Escreva as equações para corrente ic e a tensão Vr.
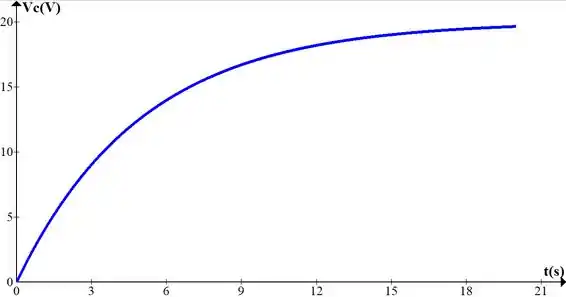
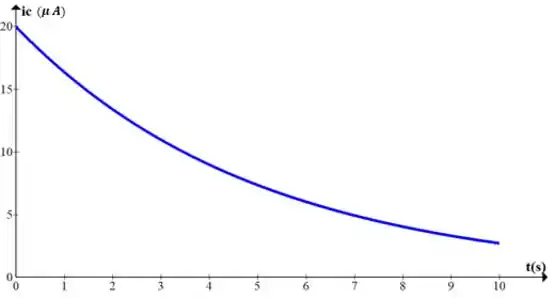
 e) Faça uma eboço das formas de onda de Vc e ic.
e) Faça uma eboço das formas de onda de Vc e ic.
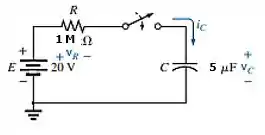
Figura 10.81 com resistor de 1 M
Passo 1
Olá galerinha! Vamos a mais um probleminha da fase de carga de um capacitor.
Mais uma vez, iniciando com a anotação das informações do problema:
Como vocês podem perceber, o problema 18 é semelhante ao 17, com uma única alteração, que é o valor da resistência. Por conta disso, vamos realizar os mesmos passos.
Passo 2
a) calcular a constante de tempo através da relação:
Passo 3
b) Agora vamos encontrar a expressão matemática para a tensão para a constante de tempo de terminada no item anterior. A expressão geral para é dada por:
Agora, basta inserir as informações que temos sobre o problema, assim chegamos à:
Passo 4
c) Agora vamos determinar a tensão para os tempos .
Aqui podemos fazer a mesma análise, pois o item é exatamente igual ao do problema anterior, para isso temos:
Dessa forma, o expoente da exponencial, para cada instante, será o valor inteiro obtido acima. Sendo assim temos:
Percebam que esse passo, como não depende do valor de t e diretamente, obtivemos os mesmos valores do problema 17.
Passo 5
d) Escrever a equação para a corrente . De forma análoga ao que foi feito para a tensão , vamos inserir as informações que temos na equação geral da corrente, que é representada por:
Desta forma, obtemos:
Passo 6
Ainda no mesmo item, o livro pede que a expressão matemática para , então inserindo as informações na equação, temos:
Passo 7
Resposta
a)
b)
c) ; ;
d) ;