Repita o Problema 12 considerando o sistema visto na Figura 19.50.
Passo 1
Faaala galerinha, como estão? Partiu resolver mais essa questão?
Primeiramente, calcularemos a potência ativa total do circuito (potência em ). Para isso, somaremos todas as potências ativas da série.
Passo 2
Agora faremos o cálculo da potência reativa, que é a parte da potência que é empregada nas cargas capacitivas e indutivas sem realizar trabalho efetivo. Sua unidade de medida é o volt ampére reativo (VAR).
Passo 3
Na sequência, faremos o cálculo da potência aparente que é a potência total que uma determinada fonte é capaz de entregar. Para definir utilizaremos a fórmula
Fechando o enunciado (a), calcularemos o Fator de Potência. O é dado por:
Passo 4
O enunciado (b) pede o cálculo da corrente . Usaremos .
Logo:
Passo 5
O triângulo de potências tem como cateto adjacente à a potência ativa , como cateto oposto a potência reativa e como hipotenusa a potência aparente . Como , temos:
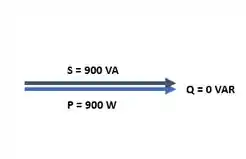
Passo 6
Realizaremos, agora, o enunciado (d), utilizando o diagrama com essas configurações:
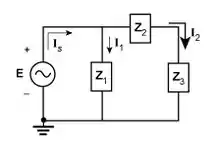
Carga 1():
Carga 2():
Carga 3(:
Passo 7
Podemos verificar se o resultado da parte (b) está correta, encontrando a corrente a partir da tensão de entrada e o resultado da resistência que será a soma dos valores encontradas no item (d)., a partir da seguinte fórmula:
A partir do valor encontrado, vemos que é menor do que o encontrado no item (b).
Resposta
a.
b.
c.
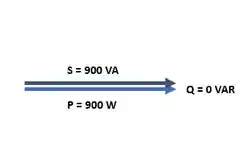
d.
e.