Repita o problema 31 para as formas de onda da figura 13.88
Passo 1
Olá galera! tudo bem?
Antes de resolver essa questão, vamos só lembrar a expressão geral de uma senóide:
Onde:
é a amplitude senoidal
ω indica a frequência angular
Corresponde ao ângulo de fase
Bora começar então resolver nossa questão.
Primeiro Lembremos de forma sucinta o gráfico da primeira alternativa.
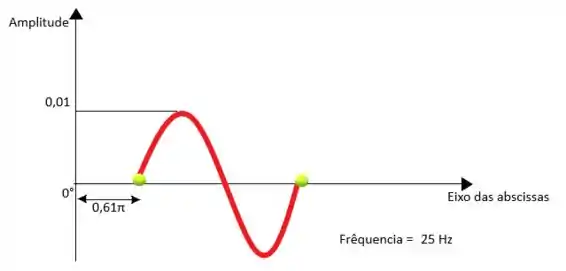
Do gráfico observado que 0,01 é a amplitude da função, e que é o ângulo de fase, para substituir na expressão geral temos que transformá-lo para grau.
Vamos só lembra que essa transformação faz por regra de três beleza
Radiano Grau
π ------------------- 180°
0,61π-------------------- x
Aplicando meio por extremos, teremos:
x.π =0,61π.180
Observe que aparece dos dois lados então vou eliminar ele da jogada, beleza!
Bora Continuar!
X= 0,61 x 180
X= 109,8°
Logo iano equivale a 109,8 ° graus.
Por fim mais não menos importante, falta encontrar a frequência angular.
Lembra da formula?

Relaxa!
Substituindo os valores, teremos:
ω= 157,07
Quase acabando!
Substituindo todos os dados na expressão
Ei? Porque o sinal do argumento da função ficou negativa?
Siga minha astucia!
A função está adiantada, só por isso.
Beleza!
Vamos para próxima alternativa.
Passo 2
(b) Agora vamos fazer a mesma coisa do passo anterior. Primeiramente vamos observar o gráfico.
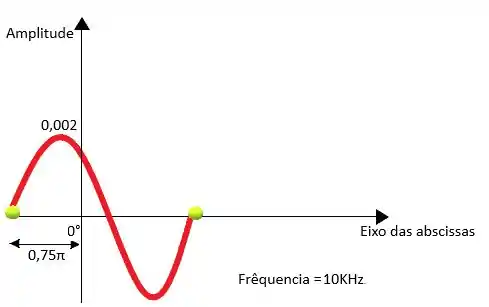
Do gráfico observado temos que 0,002 é a amplitude da função, e que é o ângulo de fase, para substituir na expressão geral temos que transforma-lo para grau.
Vamos só lembra que essa transformação faz por regra de três beleza
Radiano Grau
π ------------------- 180°
0,75π-------------------- x
Aplicando meio por extremos, teremos:
x.π =0,75π.180
Observe que aparece dos dois lados então vou eliminar ele da jogada, beleza!
Bora Continuar
X= 0,75 x 180
X= 135°
Logo iano equivale a 135 ° graus.
Por fim mas não menos importante, falta encontrar a frequência angular.
Utilizando a fórmula
Substituindo os valores, teremos:
Lembrete 25 KHz = 25000 Hz
Vamos montar nossa expressão matemática
Logo:
Prontinho, acabamos te vejo na próxima questão!
Resposta
(a)
(b)