Repita o Problema 1 para a função senoidal a seguir e compare os resultados. Determine as frequências das formas de onda nos problemas 1 e 2 e compare os valores das derivadas.
Passo 1
Opaa, bora primeiro plotar a função dada na questão para um período completo. Se liga como fica:
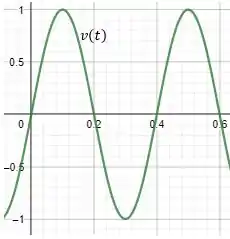
Passo 2
A gente sabe que a derivada de uma senoide é dada da seguinte forma:
Dessa forma, aplicando a derivada na equação dada no enunciado, temos:
Plotando essa derivada no mesmo gráfico mostrado anteriormente, a gente vai ter:
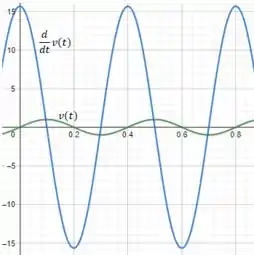
Se você analisar os pontos de máximo e mínimo da função , verão que v(t) será sempre zero. Entendeu não? Apoi se liga aqui, meu consagradx:
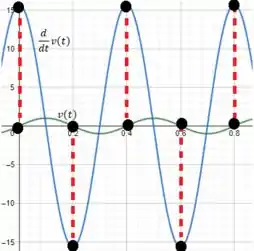
Agora sim, né? Facinho facinho ;)
Passo 3
Podemos encontrar a frequência a partir da seguinte equação:
Do Problema 1, . Logo:
Do Problema 2, . Logo:
Assim, podemos concluir que, quanto maior for a frequência da forma de onda, maior será a amplitude da derivada (pois o sairá para fora quando for realizada a derivada) e menor será o seu período (pois ).