Repita o Problema 24 se as resistências da carga forem substituídas por resistências de em série com as reatâncias capacitivas de.
Passo 1
Boraaa galerinha, aniimaaa, vamos resolver mais um!!
Só bora então!!
A resistência de cada perna de uma carga equilibrada conectada em Y é
Vamos visualizar o diagrama do circuito para os dados fornecidos
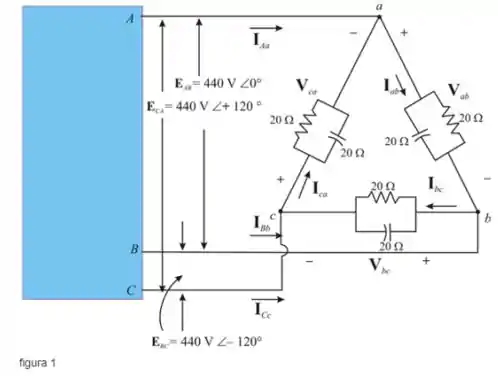
Passo 2
- Para um gerador conectado, a tensão de linha é igual a tensão de fase.
- A tensão de fase da carga é igual a tensão de fase do gerador
- A corrente de fase da carga é dada por
- Em um sistema conectado, a corrente de linha é maior que a corrente de fase por um fator de raiz quadrada de 3.
Logo, a tensão de fase do gerador é
Passo 3
Logo, a tensão de fase do gerador é
Passo 4
Portanto, a corrente de fase da carga é .
Passo 5
Portanto, a corrente de linha da carga conectada é de .
Resposta
- Portanto, a corrente de fase da carga é .
- Portanto, a corrente de linha da carga conectada é de.