Repita o Problema 13 se as resistências da carga forem substituídas por resistências de em série com reatâncias indutivas de .
Passo 1
Falaaaaaa pessoal, show de bola??
Bora resolver esse exercício na maciotaaaaa, então siimboraa!!
- Para uma sequência de fases abc,
- A tensão através da impedância de cada fase na forma de fasor é
- O diagrama fasorial das tensões é mostrado a seguir na figura.
- A tensão de linha de um sistema conectado em delta é igual à tensão de fase.
- No sistema conectado em delta, a relação entre a linha e a corrente de fase é dado como:
- A magnitude da tensão do gerador é dado como
Portanto, os ângulos de fase para a sequencia de fase especificada é .
Passo 2
Portanto, a tensão através da impedância de cada fase na forma de fasor é
Passo 3
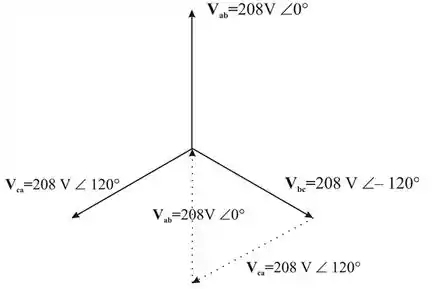
A soma dos fasores das tensões é zero, pois os três fasores formam um triângulo vetorial fechado, como mostrado na figura.
Passo 4
As impedâncias de fase são
A corrente da fase ab em forma de fasor é dada como
Portanto, a corrente é .
A corrente através da fase bc em forma de fasor é dada como
Portanto, a corrente é .
A corrente através da fase ca em forma de fasor é dada como
Portanto, a corrente é .
Passo 5
A magnitude das correntes de linha é
Portanto, a magnitude da corrente de linha é
Passo 6
Portanto, a tensão de fase do gerador é .
Resposta
- Portanto, os ângulos de fase para a sequencia de fase especificada é .
- Portanto, a tensão através da impedância de cada fase na forma de fasor é
- A soma dos fasores das tensões é zero, pois os três fasores formam um triângulo vetorial fechado, como mostrado na figura. (Vide a figura no passo 3).
- Portanto, a corrente é.
- Portanto, a magnitude da corrente de linha é .
- Portanto, a tensão de fase do gerador é .
Portanto, a corrente
Portanto, a corrente .