Repita o problema 29 para os seguintes Pares:
a) ,
b) ,
c) ,
Passo 1
Saudações galerinha! tudo bem?
Antes de resolver essa questão, vamos só lembrar a expressão geral de uma senóide:
Onde:
é a amplitude senoidal
ω indica a frequência angular
Corresponde ao ângulo de fase
Pra te lembrar ainda mais vou te mostrar o gráfico da função senoidal com a expressão geral (1) acima.
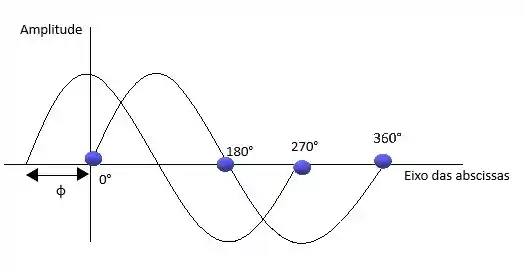
Neste caso os ângulos estão em graus
Bora começar então resolver nossa questão.
(a) Em nossa primeira alternativa temos duas funções diferentes uma seno e outra cosseno.
Para começar a analisar a relação de fase devo transformar a função em seno.
Para isso vou utilizar a transformação trigonométrica

Calma! Essa transformação trigonométrica é tranquila, borá lá aplicar
Prontinho, falei que era fácil!
Agora sim, vamos observar os ângulo de fase de , ou seja ambas as funções possuem o mesmo ângulo. Portanto essas duas funções estão em fase
Fácil de Mais né!
Vamos para a próxima alternativa.
Passo 2
(b) Nesta alternativa temos , se olharmos bem a amplitude é negativa, mais esse sinal não pertence a amplitude e sim a função seno. Neste caso temos que reescrever essa função.
Só assim poderemos encontra seu real ângulo de fase.
Borá lá remover esse sinal negativo da amplitude.
Prontinho.
Que tal montar o gráfico para analisar melhor os ângulos de fase?

Vamos só lembrar o ângulo de fase de , esses negativos significa que ambas estão adiantadas. Como assim?
Observemos o gráfico
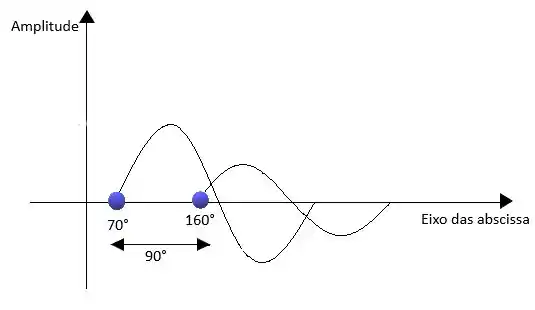
Com o gráfico atentamos que está 90° adiantada em relação a , assim como está 90° atrasada com relação a .
BELEZA, te Vejo na próxima alternativa!
Passo 3
(c) Última, UFA!
Nessa última temos a união de dois problemas
1º a função não está escrita como função senoidal
2º a amplitude de ambas está negativa
E AGORA? Relaxa!
Dividir para conquistar
Vamos primeiro escrever a função cosseno como seno, para isso vamos utilizar a identidade
Aplicando em nossa alternativa, teremos:
Prontinho! Primeiro problema resolvido, nossa função agora é:
Agora vamos eliminar esse sinal negativo da amplitude.
Ou seja o ângulo de fase é 0°
Na função , temos só que eliminar o sinal negativo da amplitude.
Siga minha astúcia, nesse último passo! .
UFA!
Vamos agora esboçar nosso gráfico, lembrando que esse sinal negativo significa que a função está adiantada 170 °.
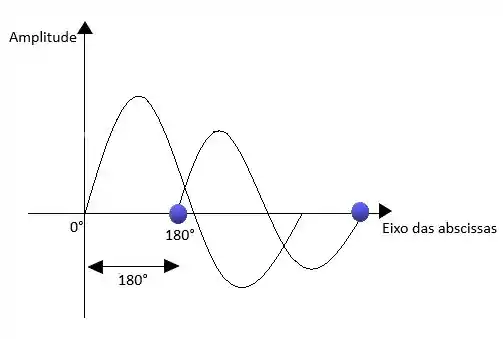
Se olhamos possui zero como fase, signica que ele está 180° adiantado em relação a .
Resposta
Ei, a resposta está no passo a passo :)