A resistência de um resistor real depende da resistência nominal e da tolerância de acordo com a equação
Em que é a resistência nominal e é a tolerância da resistência expressa como uma porcentagem. Assim, por exemplo, a resistência de um resistor de com uma tolerância de 2% é dada por:
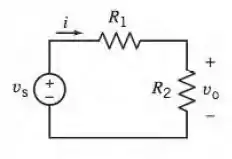
O circuito da figura P 2.4-9 possui uma entrada e uma saída . O ganho do circuito é dado por:
Determine a faixa de valores possíveis do ganho quando é a resistência de um resistor de 100 Ω. 2% e é a resistência de um resistor de 400 Ω. 5%. Expresse o ganho em termos de um ganho nominal e uma tolerância do ganho.
Passo 1
Eaí galera, bora iniciar mais uma questãozinha do nosso livro de circuitos!
Primeiro iremos determinar o valor de resistência máxima e mínima de cada resistor a partir da equação:
Para , temos:
Para , temos:
Passo 2
Após isso, nós temos que o ganho do circuito é dado por:
E quando substituímos os valores em , temos:
Dessa forma temos: