Sabemos que a carga de um condutor vai para a superfície, mas não é fácil determinar exatamente como ela se distribui. Um exemplo famoso no qual a densidade de carga superficial pode ser explicitamente calculada é o elipsoide:
Neste caso
Onde é a carga total. Escolhendo valores apropriados para obtenha (a partir da Equação 2.57):
a) a densidade líquida (de ambos os lados) da carga superficial em um disco circular de raio ;
b) a densidade líquida da carga superficial em uma ‘fita’ condutora infinita no plano que se sobrepõe ao eixo entre e (considere que é a carga total por unidade de comprimento da fita);
c) a carga líquida por unidade de comprimento em uma ‘agulha’ condutora que fica entre e . Em cada caso, desenhe o gráfico do seu resultado.
Passo 1
a) Faala, pessoal! Bora pra mais uma. Para calculara densidade líquida da carga superficial em um disco circular, vamos primeiro eliminar a variável , e utilizando a fórmula da densidade para um elipsoide, teremos:
E agora, como temos que a variável também será , ou seja, temos uma elipse no plano :
Como devemos levar em conta os dois lados do elipsoide, vamos multiplicar a expressão por 2:
Agora, como no item a) nos foi pedido que calculássemos a densidade de carga para um disco circular de raio , teremos que e Aplicando na expressão anterior:
O gráfico será:
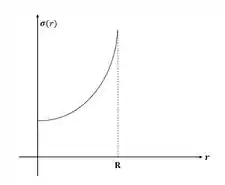
Passo 2
b) Para uma fita condutora infinita no plano , teremos que (como dito no enunciado) e como devemos considerar comprimento infinito , vamos ter:
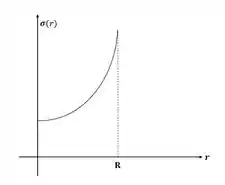
O gráfico será:
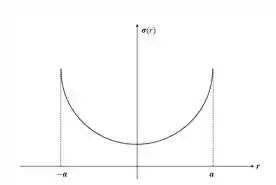
Passo 3
c) Para uma agulha condutora, teremos que e para termos um elipsoide de revolução, portanto, ficaremos com:
A densidade de carga será, então:
A carga líquida por unidade de comprimento é dada por:
A carga para um anel de largura é:
Onde:
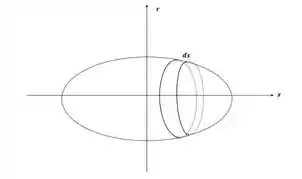
Derivando a expressão do elipsoide, teremos:
Logo:
Substituindo esse resultado na expressão para :
Agora aplicando os resultados encontrados para e na expressão inicial para a carga líquida por unidade de comprimento :
O gráfico será:
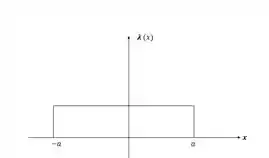
Resposta
a)
b)
c)