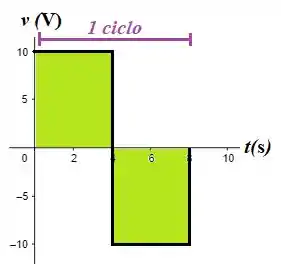
Quais são os valores médio e eficaz da onda quadrada vista na figura?
Passo 1
Chega mais aí! Vamos primeiro encontrar o valor médio! Mas o que é isso??
Bom, chamaremos o valor médio de , de tal forma que:
Dessa forma, analisando o gráfico da figura, vemos que:
Passo 2
Agora, vamos encontrar o valor eficaz ou rms!
Primeiramente, lembramos que o valor rms da forma de uma onda periódica é dado por:
Ou seja,
Em que é o período.
Passo 3
Pela figura, vemos que tratam-se de duas ondas quadradas!! Isso facilita muito na resolução pois podemos interpretar a área de um quadrado como a de um retângulo (exceto pelo fato de que o quadrado possui todos os lados iguais né haha). Como a área de um retângulo é o produto da base pela altura, é só somar as áreas de cada retângulo (os quadrados, nesse caso haha)!! ;)
Obs: Nesse caso, a altura (que será a tensão no gráfico) é elevada ao quadrado por conta da equação do valor eficaz mostrada anteriormente, não se esqueça ;)
Assim, pela equação mostrada anteriormente, temos: