Considera um sistema de referencial inercial.
- Suponha que move-se com velocidade constante em relação a Mostre que é também um sistema de referencia inercial [Dica: use a definição da nota de rodapé 1]
- Inversamente, mostre que se é um sistema inercial, ele se move com relação a a velocidade constante.
Passo 1
Faaaaaala, galera... Tranquileba??
Para resolvermos, façamos a velocidade do sistema e a velocidade no sistema ,
E a velocidade do sistema com respeito ao sistema
No sistema de referencias, algo assim:
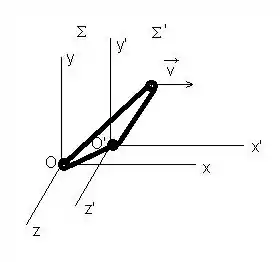
Bom, sabemos que:
E que pela primeira Lei de Newton, temos que u é constante.
Lembra da Lei de Newton?

Lady Newton
Brincadeiras à parte, bora pro próximo passo?!
Passo 2
Obrigado por vir.
Para a)
Se a relação entre S e nos dá um constante, então:
Também é constante, de forma que a primeira lei de Newton ainda permanece em sendo inercial.
Passo 3
Para b)
Se é inercial, então a sua velocidade é constante, então é constante
Resposta
Ei, a resposta está no passo a passo :)