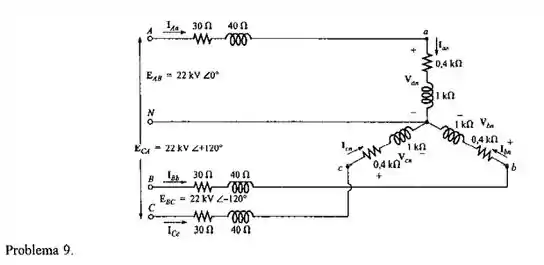
Para o sistema Y-Y visto na Figura 22.41:
- Calcule o módulo e o ângulo de fase associados às tensões .
- Determine o módulo e ângulo de fase associados às correntes de fase .
- Calcule o módulo e o ângulo de fase associados às correntes de linha .
- Determine o módulo e o ângulo de fase das tensões de fase .
Passo 1
E ai seres de luz, tudo bem?
Bora resolver mais uma?
Encostaaa!!
Consultando a Figura no livro texto, temos
As tensões de linha são
A impedância em cada fase da carga conectada em Y é
em série com
A impedância de linha é
Passo 2
- Em um sistema conectado em Y, a tensão de linha é maior que a tensão de fase por uma fator de
- Calculando a corrente de fase da carga
- Em um sistema conectado em Y, a corrente de fase e as correntes de linha são as mesmas, ou seja
- Vamos calcular a tensão de fase da carga
Ou seja
Sabendo que o ângulo de fase entre a tensão de fase e a tensão de linha é de 30°
Calculando a tensão de fase , do lado do gerador
Portanto, as tensões de fase no lado do gerador é:
Passo 3
Calculando a corrente de fase da carga
Calculando a corrente de fase da carga
Portanto, as correntes de fase da carga é
Passo 4
Pela imagem 22.41, temos que as correntes de linha são
Portanto, as correntes de linha são
Passo 5
Vamos calcular a tensão de fase da carga
Vamos calcular a tensão de fase da carga
Portanto, as tensões de fase em cada fase da carga é
Resposta
- Vide o passo 2.
- Vide o passo 3.
- Vide o passo 4.
- Vide o passo 5.