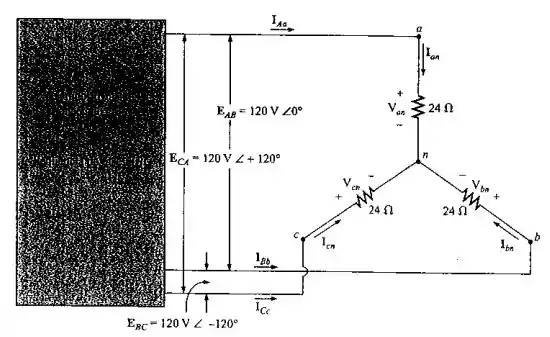
Para o sistema visto na Figura 22.45, determine o módulo das tensões e correntes desconhecidas.
Passo 1
E ai seres de luz, tudo bem?
Bora resolver mais uma?
Encostaaa!!
Pela figura do enunciado, podemos inferir os seguintes dados
As tensões de linha de um gerador trifásico conectado a 3 fios
A impedância de cada fase da carga conectada em Y é
Passo 2
Em uma carga conectada em Y, a relação entre a tensão de linha e a tensão de fase é dada por
Portanto, as tensões de fase são
A tensões de fase das cargas são
Passo 3
As correntes de fase da carga conectada em Y são dadas como
Portanto, as correntes de fase da carga conectada em Y são
Passo 4
Na carga conectada em Y, a corrente de linha é igual à corrente de fase; Portanto, as correntes de linha de carga são
Resposta
A tensões de fase das cargas são
Portanto, as correntes de fase da carga conectada em Y são
Na carga conectada em Y, a corrente de linha é igual à corrente de fase; Portanto, as correntes de linha de carga são