- Substitua a configuração vista na Figura 8.126 (composta de resistores de ) por uma configuração .
- Calcule a corrente fornecida pela fonte .
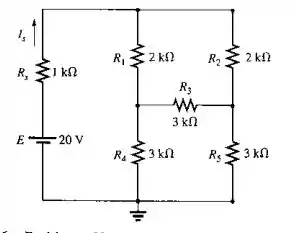
Passo 1
Falaaaaaa pessoal, show de bola??
Bora resolver esse exercício na maciotaaaaa, então siimboraa!!
- Como as resistências na configuração dadas são as mesmas, as resistências na configuração T equivalente também são as mesmas.
- Nas resistências do circuito acima estão em serie e , e . Portanto , seu equivalente em série é dado por
Portanto:
Portanto o circuito da configuração e dada por
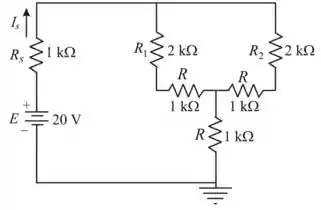
Passo 2
Redesenhando
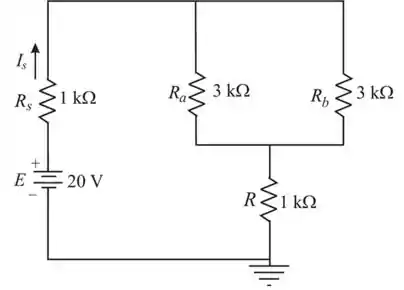
Passo 2
A combinação paralela de resistências, está em serie com a resistência R. Portanto, seu equivalente é
Redesenhando
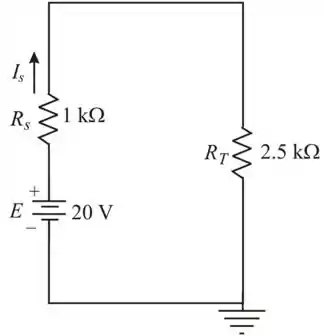
A corrente da fonte é dado por
Resposta
- Vide o passo 1.