Uma superfície cônica (um cone de sorvete vazio) tem uma densidade de carga uniforme . A altura do cone é , assim como o raio do topo. Encontre a diferença de potencial entre os pontos (o vértice) e (o centro do topo).
Passo 1
Falaaa, tudo belezaa?? Para encontrarmos essa diferença de potencial vamos calcular o potencial em cada ponto e depois subtrai-los.
A fórmula para o potencial que vamos usar está abaixo:
O que precisamos fazer agora, então, é definir as variáveis e calcular a integral. Bora lá!!
Passo 2
As variáveis do cálculo podem ser analisadas abaixo:
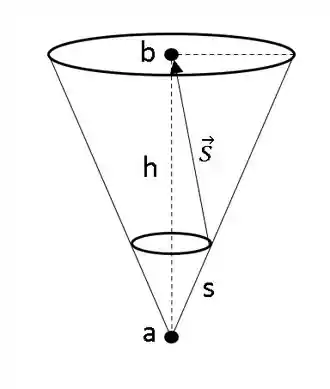
Calculando o potencial elétrico em .
Onde .
Calculando o potencial elétrico em .
Onde e .
Calculando a diferença de potencial entre os dois pontos, encontramos: