Suponha que você quer encontrar o campo de um Circuito circular (Exemplo 5.6) em um ponto r que não está diretamente acima do centro (Figura 5.61). É preferível escolher os eixos de forma que r fique no plano em O ponto fonte é e d vai de 0 a . Monte as integrais a partir das quais você poderia calcular e calcule explicitamente B.
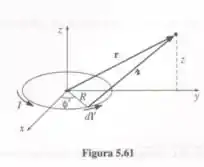
Passo 1
Olá pessoal bora para mais uma!?
Para começar a resolver está questão podemos partir de:
Onde , ressaltando também que:
Ou melhor escrevendo, temos que:
Temos as coordenadas de origem para satisfazer, temos que:
Assim temos que:
Passo 2
Agora podemos fazer o produto vetorial da equação do campo magnético, assim temos que:
Passo 3
E assim podemos encontrar as integrais para assim temos:
Agora podemos expressar
Assim finalizamos mais uma questão! Até a próxima!