Para a tela de um osciloscópio ilustrada na figura 13.91, determine:
- Os períodos das duas ondas.
- As frequências das duas ondas.
- Os valores eficazes das duas ondas.
- A diferença de fase entre as duas ondas.
Passo 1
Bora lá galera, vamos juntos resolver mais um exercício!
Antes de tudo vamos observar uma figura parecida com a mostrada no livro como sendo na tela do osciloscópio, essa figura nos dá informações importantes.
Primeiro as sensibilidades. O que significa isso?
Que cada quadrado vertical valerá 0,5 V e Horizontal 1ms.
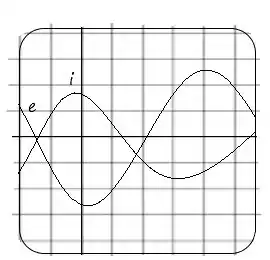
DADOS:
Sensibilidade Vertical = 0,5 V/ div
Sensibilidade Horizontal = 1 ms/ div
Acho que estamos prontos para começar
Bora lá
Passo 2
- Na alternativa ele quer saber o período que é encontrado observando o eixo horizontal, ou seja até onde a curva completar 1 ciclo.
- Para encontrar a frequência basta utilizar a relação (1):
- Nessa alternativa temos que relembrar como calcular tensão, pois em nosso exercício e corresponde a uma tensão.
Observamos que 8 quadrados formam um ciclo da onda e 8 quadrados também formam o ciclo da onda Logo para encontrar o período da onda, basta multiplicar a quantidade de quadrados pelo valor de cada um no eixo horizontal.
Período = 8 x 1ms
O Período de ambas as ondas é 8 ms
Passo 3
Como ambas possuem o mesmo período basta calcular a frequência apenas uma vez.
Vamos para próxima alternativa, siga minha astúcia!
Passo 4
Relembrando teremos:
A tensão eficaz (Veff) = Vmáx . 0,707
Lembrou?
Massa, bora continuar então!
Observando a no osciloscópio, a tensão máxima é fornecida com o eixo vertical, logo
Percebemos que ela ocupa 1 quadrado e meio verticalmente ou seja:
1,5 (equivale a quantidade de quadrados ocupadas) x (valor do quadrado vertical)
V máx = 1,5 . 0,5
V máx = 0,75 V
Portanto a tensão eficaz será:
Veff = Vmáx . 0,707
Veff =0,75. 0,707
Veff = 0,530 V
Fixamos nosso olhar em , no osciloscópio tensão máxima é fornecida com o eixo vertical, logo Percebemos que ela ocupa 2 quadrado e meio verticalmente ou seja:
2,5 (equivale a quantidade de quadrados ocupadas) x (valor do quadrado vertical)
V máx = 2,5 . 0,5
V máx = 1,25 V
Portanto a tensão eficaz será:
Veff = Vmáx . 0,707
Veff =1,25 . 0,707
Veff = 0,883 V
Passo 3
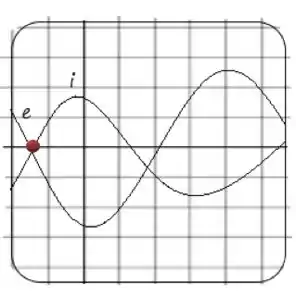
(d) Em nossa última alternativa temos que observar as funções e encontrar a diferença de fase. Vejamos o gráfico mais uma vez.
Agora destacamos um ponto em especial (em vermelho), as duas funções começam no mesmo ponto sendo totalmente contrarias, quando isso ocorre afirmamos que a diferença de fase entre ambas é 180°
Ufa essa foi longa, mas terminamos.
Te vejo na próxima questão!
Resposta
- Período 8 ms
- Frequência 125 Hz
- Tensão eficaz 0,883 V e 0,530 V
- Diferença de fase é 180°