A tensão inicial no capacitor visto na Figura 24.57 é 5 V, com a polaridade indicada na figura. A chave é fechada em t = 0 s.
a. determine a expressão matemática para ;
b. faça o gráfico de em função do tempo;
c. determine a expressão matemática para a corrente ;
d. faça o gráfico de em função do tempo.
Passo 1
Bem vindos pessoal de exatas!
Vamos lembrar como se calcula a tensão no capacitor
observando a polaridade e a figura, vou listar as informações contidas nela
Beleza, temos tudo que precisamos. Só substituir os valores
Passo 2
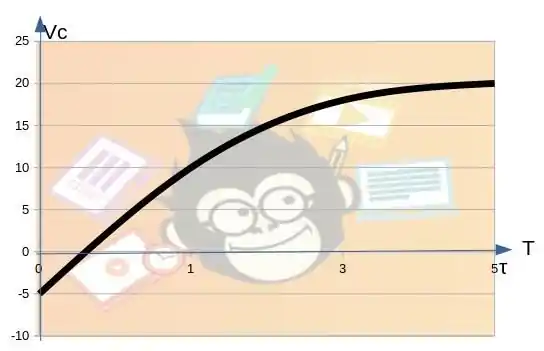
Sabemos que a tensão inicial é -5 V
e se elevarmos ( a um número negativo muito grande, então (Vc ) irá tender a 20
Passo 3
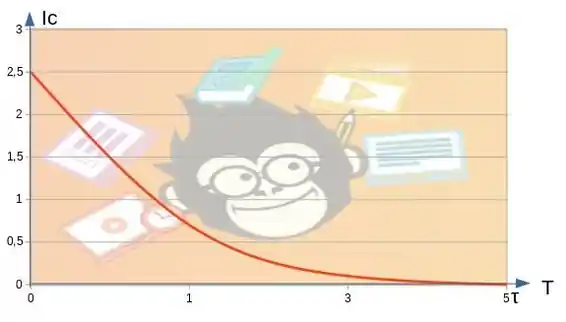
Uma das formas de se obter a corrente é
temos esses valores, então já podemos resolver
Dessa vez, quando aumentamos o valor de (t) a expressão tende a 0
Resposta
a
b. Gráfico no passo 2
c
d. Gráfico no passo 3