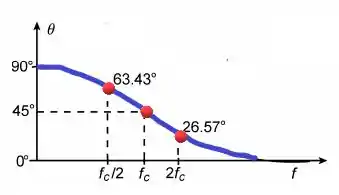
a) Trace o gráfico de Bode de para um filtro passa – alta mostrado na figura
b) Com base nos resultados do item (a), desenhe a curva de resposta real para a mesma faixa de frequência.
c) Determine o ganho dB para
d) Determine o ganho para .
e) Trace a curva de resposta de fase para a mesma faixa de frequência.
Passo 1
Oi galerinha, tudo bem?
Vamos juntos resolver mais um exercício!
a) Em nossa primeira alternativa temos apenas que desenha um gráfico de Bode genérico para um filtro passa –alta.
Seu esboço genérico está abaixo:
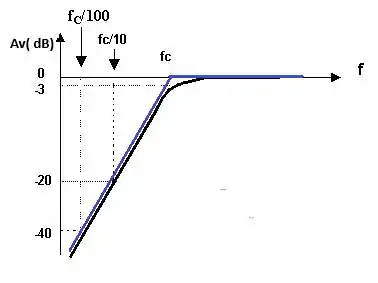
Prontinho, vamos para nosso próximo item!
Passo 2
b) Agora devemos completar nosso esboço do item anterior calculando a frequência de corte.
Só lembrando que a relação para a frequência de corte é:
Substituindo com os valores fornecidos na questão teremos:
Preenchendo nosso gráfico com o valor da frequência de corte vamos obter:
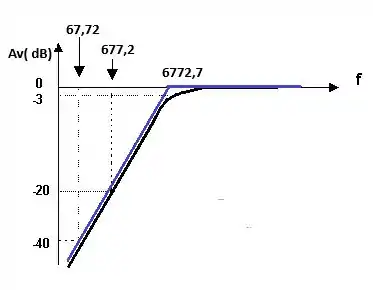
Temos ainda o próximo item !

Passo 3
c) Agora devemos encontra para isso devo utilizar a equação:
Lembrou? Tudo tranquilo vamos continuar então!
Calculado o ganho para diversas frequências, beleza!
Para
Para
Para
Para
Passo 4
d) Nesse item vamos continuar com o mesmo raciocínio do item anterior, mas agora o ganho não é . Na verdade muda pouca coisa, inclusive na equação que se torna:
Mão na masa então, quase acabando!
Para
Para
Passo 5
Oba, último item!
e) Esboça a resposta da frequência para esse circuito, tranquilo né!
Só lembrando que
Para
Para
Para
Aplicando nossas informações, nosso gráfico ficará assim.
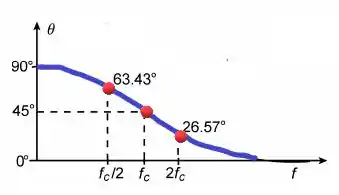
Ufa terminamos, te vejo na próxima!
Resposta
a)
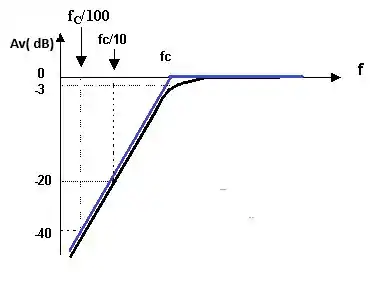
b)
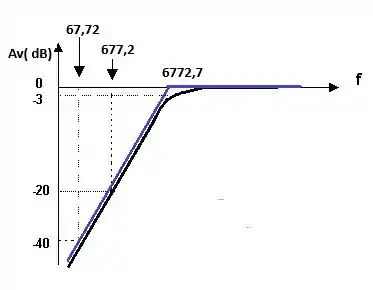
c)
d)
e)