a) Trace um gráfico do módulo de ( em termos de em função da frequência para o filtro passa –alta visto na figura
b) A partir dos resultados do item (a), trace a curva para a mesma faixa de frequência.
c) Troce o gráfico de Bode.
d) Trace a curva real, indicando a diferença em dB, entre a curva idealizada e real para
e) A partir do gráfico do item (d), determine para e o vaor correspondente a .
f) Trace a curva de fase (ângulo em que está adiantada em relação a ) para a mesma faixa de frequência.
Passo 1
Olá galerinha, tudo bem?
Vamos juntos resolver mais um exercício!
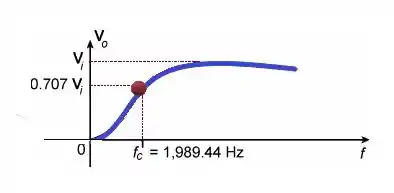
a) Em nossa primeira alternativa temos apenas que desenha um gráfico de Bode para um filtro passa –alta.
Antes de esboça-lo temos que encontra a frequência de corte, tranquilo!
Só lembrando que a relação para a frequência de corte é:
Mas se olharmos para a figura percebemos que devemos calcular a resistência equivalente, pois o circuito tem dois resistores em paralelo.
Vamos lá calcular então!
Substituindo os valores, vamos obter:
Substituindo com valores fornecidos na questão conseguimos calcular a frequência de corte:
Relacionando a frequência de corte com o ganho temos:
Isolando :
Agora estamos prontinho para esboçar nosso gráfico, tudo bem aí ?
Nosso gráfico ficará assim.
Passo 2
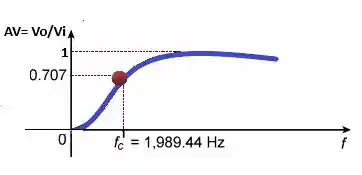
b) Nossa próxima alternativa vamos ter quer fazer o gráfico agora, em termos do ganho , praticamente temos que mudar o eixo vertical.
Nosso gráfico ficará assim:
Tranquilo até aí?

Passo 3
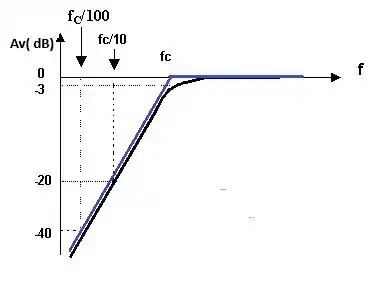
c) Nesta alternativa temos apenas que desenha um gráfico de Bode genérico para um filtro passa –alta.
Seu esboço genérico está abaixo:
Prontinho, vamos para nosso próximo item!
Passo 4
Agora devemos completar nosso esboço do item anterior adicionando a frequência de corte já calculada tranquilo!
Só lembrando que a frequência de corte calculada foi:
Preenchendo nosso gráfico com o valor da frequência de corte vamos obter:
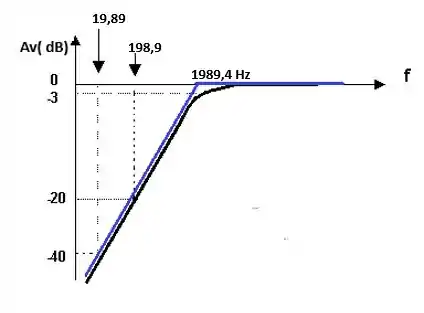
Temos ainda alguns item, bora lá!
Passo 5
e) Para determinar tenho que lembrar qual a sua relação com :
Para refrescar nossa memória a relação entre dois está descrita abaixo:
Em nosso exercício o ganho , substituindo na relação acima:
Passo 6
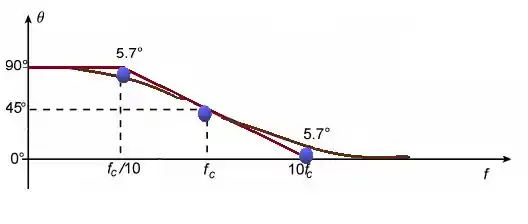
f) Por fim! Mas não menos importante último item.
Esboça a resposta da frequência para esse circuito, tranquilo né!
Só lembrando que
Para
Para
Para
Aplicando nossas informações, nosso gráfico ficará assim.
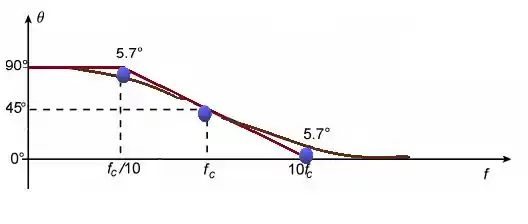
Ufa terminamos, te vejo na próxima!
Resposta
a)
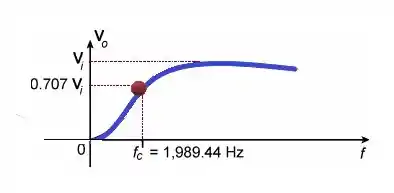
b)
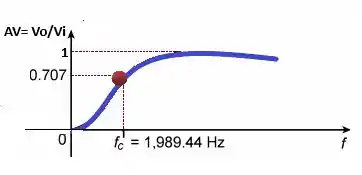
c)
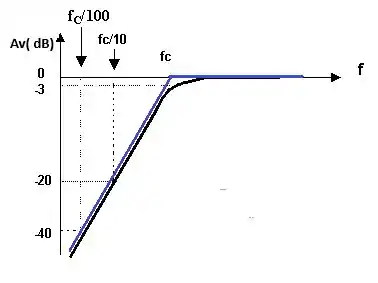
d)
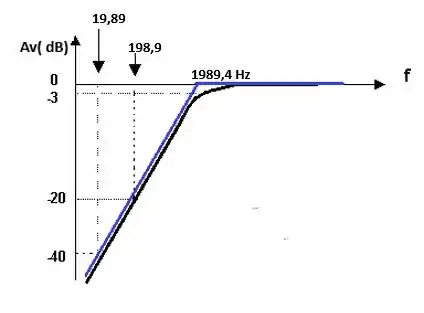
e)
f)