a) Trace o gráfico do módulo de (em termos de ) em função da frequência para o filtro passa-baixa visto na Figura
b) Com base no resultado do item (a), trace a curva de para a mesma faixa de frequência.
c) Trace o gráfico de Bode idealizado.
d) Trace a curva real, indicando a diferença em dB, entre a curva real e a curva de Bode para
e) A partir do gráfico do item (d), determine para e o valor correspondente de
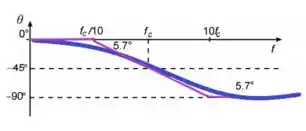
f) Trace a curva de fase (ângulo no qual está adiantada em relação a ) para a mesma faixa de frequência.
Passo 1
Oi galerinha, tudo bem?
Vamos juntos resolver mais um exercício!
a) Nesta alternativa temos apenas que desenha um gráfico de para um filtro passa –baixa.
Para isso é necessário encontrar a tensão de saída.
Vamos começar então!
Como temos um resistor e um capacitor devemos fazer a análise desse circuito, levando em consideração que estão em paralelo.
Aplicando nossa expressão na equação do ganho:
Para simplificar nossa vida, vamos definir que
Para f
Teremos em nossa tensão de saída ficará:
Substituindo com os valores fornecidos no circuito:
Para encontrar nossa frequência de corte usaremos nossa definição acima:
Prontinho! Vamos esboçar o gráfico agora?
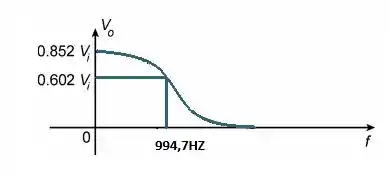
Passo 2
b) Agora devemos completar nosso esboço do item anterior escrevendo a tensão de saída em termo do ganho, tranquilo!
Preenchendo nosso gráfico com essa modificação vamos obter:
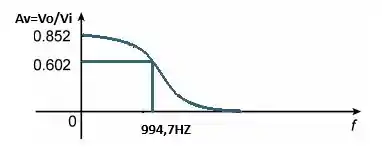
Vamos lá, siga minha astúcia próximo item!
Passo 3
c) Para o filtro passa- baixa o gráfico de bode idealizado pode ser descrito como:
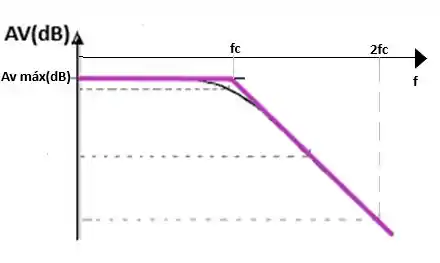
Fácil né, te vejo no próximo item:
Passo 4
d) Agora vamos preencher o gráfico de Bode do passo anterior, tranquilo?
Antes vamos só encontrar o ganho em dB utilizando a relação abaixo:
Bora lá então!
Adicionando este valor no gráfico do passo anterior vamos obter:
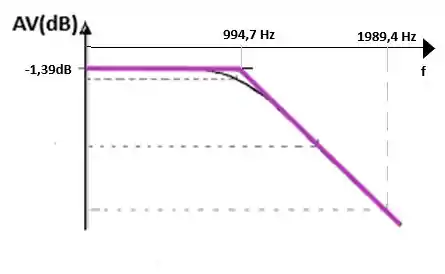
Prontinho acabamos, vamos para o próximo item!
Passo 5
e) Nessa alternativa, vamos considerar a equação do ganho abaixo para resolver:
Sabemos pelo outros item que o ganho dB será:
Aplicando na fórmula , vamos obter:
Passo 6
e) Por fim! Mas não menos importante último item.
Esboça a resposta da frequência para esse circuito, tranquilo né!
Só lembrando que
Para
Para
Para
Aplicando nossas informações, nosso gráfico ficará assim.
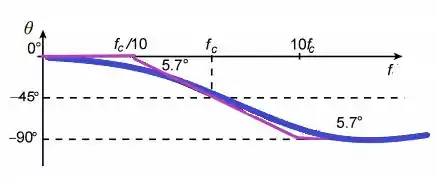
Ufa terminamos, te vejo na próxima!
Resposta
a)
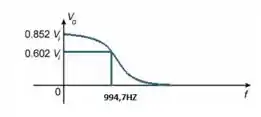
b)
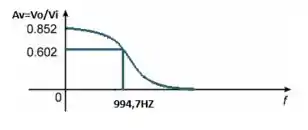
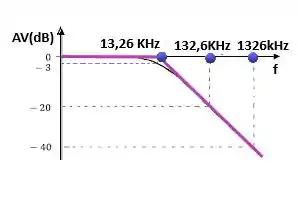
c)
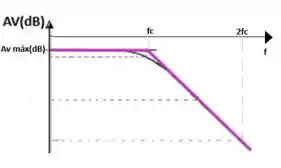
d)
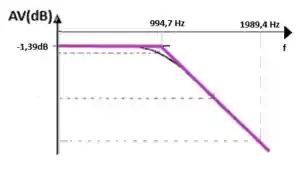
e)
f)