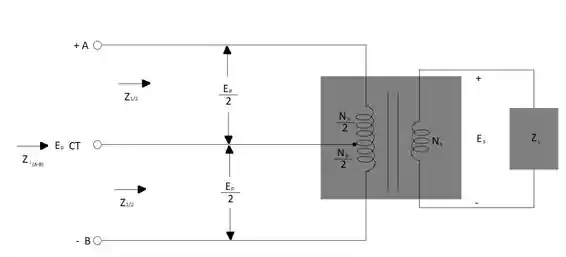
Para o transformador com derivação central visto na Figura 21.42 com Np = 100, Ns = 25, ZL = R0° = 5Ω0° e Ep = 100 V0°.
- Determine a tensão e corrente na carga.
- Encontre a impedância Zi.
- Calcule a impedância Z1/2.
Passo 1
Estamos mais uma vez aqui com vocês para responder as suas perguntas, comecemos pela letra A. Usaremos relações de tensões e correntes para o transformador indicado na figura:
Passo 2
Para encontrar a impedância que se pede na letra B se usa a relação de impedâncias da seguinte forma:
Passo 3
Para a resposta da letra C apenas se realiza o seguinte cálculo de acordo com as informações obtidas:
Finalmente terminamos a questão, não foi tão difícil não é mesmo?
Resposta
IL = 25 A0°