Para o transformador visto na Figura 21.59, determine:
a) a resistência equivalente ;
b) a reatância equivalente ;
c) o circuito equivalente refletido no primário;
d) a corrente no primário para ;
e) a tensão na carga ;
f) o diagrama de fasores do circuito refletido para o primário;
g) o novo valor da tensão na carga considerando que o transformador é ideal com uma relação de espiras de 4:1. Compare o resultado com o do item (e).
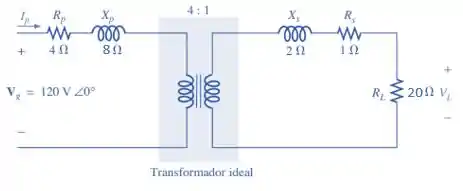
Figura 21.59
Passo 1
Oi pessoal, vamos para mais um probleminha de transformadores.
a) Para calcular a resistência equivalente , vamos utilizar a equação 21.22, escrita como:
Então, como primeiro passo, temos que calcular o fator a, descrito por:
Agora que determinamos o a, podemos calcular a resistência equivalente:
Passo 2
b) A reatância equivalente é expressa por uma equação semelhante à da resistência equivalente (eq. 21.23), descrita por:
Como já determinamos o a, podemos inserir as informações do problema na equação acima e calcular a reatância equivalente:
Passo 3
c) Esse item já foi facilitado pelos itens anteriores, onde calculamos e , logo, só temos que calcular a impedância na bobina primária. Sendo assim:
assim, podemos desenhar o circuito equivalente como:
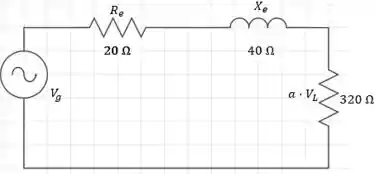
Passo 4
d) Agora para calcular a corrente, temos a equação:
Sendo , temos:
Que é equivalente a:
Isso será:
Passo 5
e) O será expresso por:
Inserindo as informações na equação acima, nós teremos:
Passo 6
f) Como há uma malha analisada, a tensão tem que corresponder a soma das tensões sobre , e , sendo que tem que estar em fase com a corrente, logo mesma direção, e a 90° de . Para ficar mais fácil, pense na soma de vetores!
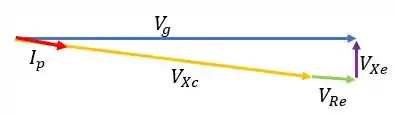
Passo 7
g) Podendo ser expresso por:
Temos,
Resposta
a) ; b)
d) ; e)
g)