Para o transformador visto na Figura 21.59, se a carga resistiva for substituída por uma reatância indutiva de :
a) Determine a impedância total refletida para o primário.
b) Calcule a corrente no primário.
c) Determine as tensões em , e na carga refletida.
d)Construa o diagrama de fasores.
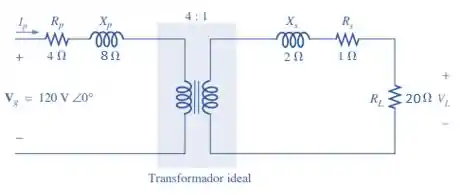
Figura 21.59
Passo 1
E aí pessoal?! 😉
a) Para calcularmos a impedância total, temos a equação abaixo:
Para nos poupar tempo, vamos utilizar as informações já calculadas no problema 14, descritas abaixo:
Só podemos utilizar essas informações, porque estamos trabalhando com o circuito semelhante, e o que diferiu de um problema para outro, não interferiu nas informações acima.
Sendo assim, podemos calcular a impedância total sem maiores problemas, basta inserir as informações na equação:
OBS.: Lembrar que neste caso a carga resistiva foi substituída pela reatância indutiva.
Desta forma teremos:
Passo 2
b) Assim como fizemos no problema anterior, vamos calcular a corrente por:
Isso nos leva à:
Passo 3
c) As tensões serão expressas como:
E,
Passo 4
d) Nos itens anteriores, já calculamos os módulos e direções, agora é só montar o diagrama:
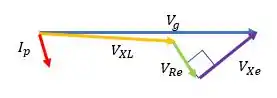
Resposta
a) ; b) ; c) , e