Usando a abordagem padronizada, escreva as equações nodais para os circuitos mostrados na Figura 8.113. Existe simetria? Usando determinantes, calcule as tensões nodais.
Passo 1
Falaaa moçadinhaaaa, show de bola?
Bora lá?
Vamos começar redesenhando a rede como mostra a Figura a seguir, ou seja figura 1.
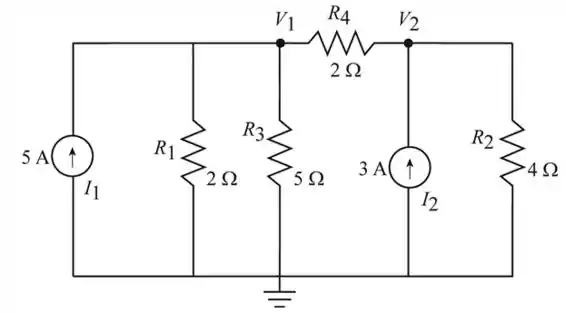
Passo 2
Vamos considerar o nó na Figura 1, e encontrar a tensão usando a análise nodal
Consideremos o nó 2, na Figura 1, e encontrar a tensão usando a análise nodal
Consideremos a seguinte formação de matriz e e encontrar a tensão usando determinantes.
Partindo dessa equação (3), iremos encontrar os valores de tensão usando determinantes
Sendo assim, os valores de tensão são
Na formação de matrizes, uma matriz simétrica é uma matriz quadrada que é igual à sua transposta.
Portanto, a simetria está presente na Figura 1.
Passo 3
Bom iremos redesenhar a rede como mostrado a seguir, Figura 2.

Passo 4
Vamos considerar o nó na Figura 2, e encontrar a tensão usando a análise nodal
Consideremos o nó 2, na Figura 2, e encontrar a tensão usando a análise nodal
Consideremos a seguinte formação de matriz e e encontrar a tensão usando determinantes.
Partindo dessa equação (6), iremos encontrar os valores de tensão usando determinantes
Sendo assim, os valores de tensão são
Na formação de matrizes, uma matriz simétrica é uma matriz quadrada que é igual à sua transposta.
Portanto, a simetria está presente na Figura 2.
Resposta
Vide o passo a passo!