Usando uma conversão , determine a corrente em cada um dos circuitos mostrados na Figura 8.122.
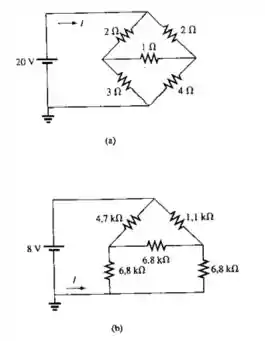
Passo 1
Alô Alô galerinha, tranquilinho?
- Vamos converter o modelo na Figura dada para o modelo .
- Vamos substituir
Considerando a seguinte fórmula e encontraremos a resistência do modelo
Passo 2
Vamos redesenhar a figura para determinar a resistência total. A rede modificada é mostrada a seguir
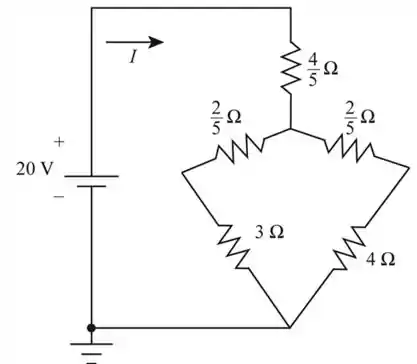
Considere a seguinte fórmula e encontre a resistência total
Passo 3
Vamos redesenhar a figura 1 para determinar a corrente. A rede modificada é mostrada a seguir
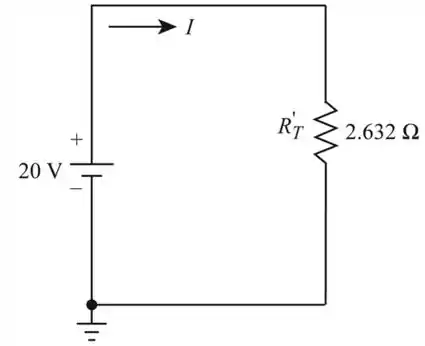
Aplicando a lei de Ohm e encontrando a corrente
Portanto, o valor atual é
Passo 4
Redesenhando
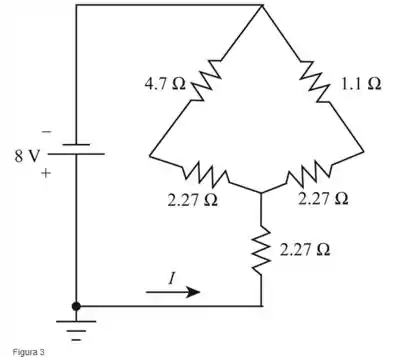
Considerando a seguinte expressão, encontraremos a resistência total
Passo 2
Redesenhando
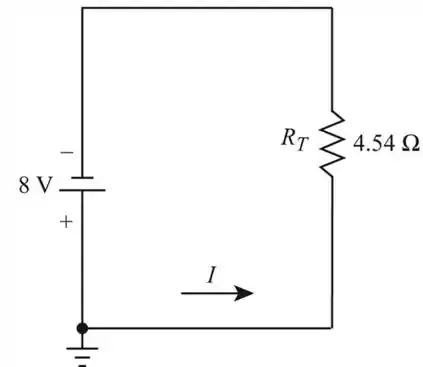
Considerando a seguinte expressão iremos encontrar a corrente
Portanto, o valor atual é de .
Resposta
- Portanto, o valor atual é
- Portanto, o valor atual é de .