Usando a leitura do osciloscópio apresentada na Figura 15.126, determine a capacitância C.
Passo 1
Faaala galerinha, como estão? Partiu resolver mais essa questão?
Primeiro passo que faremos é encontrar a Tensão Resistiva .
Portanto:
Passo 2
Nesse passo, determinaremos .
Utilizando um simples diagrama de tensões verificamos a existência de um triângulo retângulo que possui a tensão total como hipotenusa e as tensões Resistivas e Capacitivas como seus catetos:
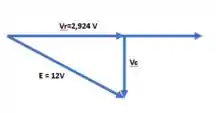
Portanto:
Passo 3
Agora, como conhecemos a Tensão e a Resistência, fica fácil calcular a Corrente:
E, utilizando uma das fórmulas de Reatância Capacitiva, calcularemos:
Passo 4
Para finalizar, utilizaremos outra fórmula de Reatância Capacitiva para determinarmos a Capacitância :
Isolando o termo :