Usando a regra dos divisores de tensão, determine (com a polaridade correspondente) para os circuitos mostrados na Figura 5.85.
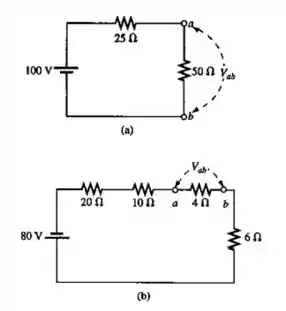
Passo 1
Falaaaaaaaaaai meus amorecosss, show de bola?
Bora pra mais uma?
- Usaremos a fórmula e iremos encontrar
- Vamos substituir os valores numéricos e encontrar
- Vamos substituir os valores numéricos e encontrar
- Vamos substituir os valores numéricos e encontrar
Portanto, o valor de e a polaridade de a é e para b é .
Passo 2
Portanto, o valor de , e a polaridade de a é e para b é .
Passo 3
Portanto, o valor de , e a polaridade de a é e para b é .
Passo 4
Portanto, o valor de , e a polaridade de a é e para b é .
Resposta
- Portanto, o valor de e a polaridade de a é e para b é .
- Portanto, o valor de , e a polaridade de a é e para b é .
- Portanto, o valor de , e a polaridade de a é e para b é .
- Portanto, o valor de , e a polaridade de a é e para b é .