a) Usando resistores de 1 kV e amp op ideais, projete o filtro Butterworth passa-baixas especificado no Problema 15.34. O ganho é unitário na faixa de passagem.
b) Faça o diagrama do circuito, identificando todos os valores dos componentes.
Passo 1
- A frequência de corte não escalonada é dada por,
a frequência de corte escalonada é dada por,
Então, o fator de escala de frequência Kf é dado por,
Sejam os valores dos resistores não escalonados R e do capacitor C do circuito de primeira ordem:
Determine o fator de escala de magnitude
onde R’ é o resistor escalado dado.
Determine o capacitor escalado C',
Os resistores não escalonados de segunda ordem R, capacitor e capacitor são dados b,
onde é o coeficiente de s no polinômio de segunda ordem.
O resistor escalado é,
Determinando a capacitância
e agora determinando
Passo 2
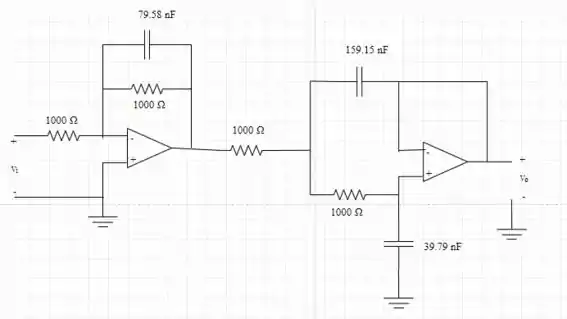
Resposta
- Olhar a figura