Usando o teorema da superposição, determine a corrente nos circuitos vistos na figura 18.110.
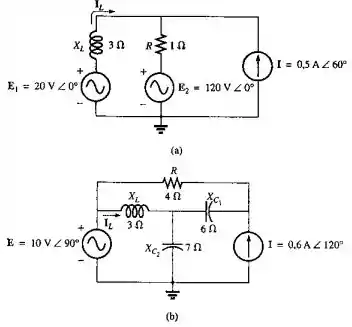
Passo 1
Fala, galera! Bora resolver mais uma questão de circuitos?
Vamos começar pela letra A. Primeiramente, vamos listar as impedâncias do circuito:
Podemos então aplicar o teorema da superposição. Lembrem-se que quando desligamos uma fonte de tensão, devemos substituí-la por um curto circuito, e ao desligar uma fonte de corrente, devemos inserir um circuito aberto em seu lugar.
Desligando as fontes e , teremos e em série. Logo, basta aplicarmos a lei de Ohm para descobrir a corrente que passa por essas impedâncias:
Desligando as fontes e , teremos novamente e em série. Pela lei de Ohm, temos que:
Por fim, desligando as fontes e , teremos e em paralelo. Note que agora teremos um divisor de corrente:
Prontinho! Somando os resultados das três análises, teremos:
Passo 2
Vamos para a letra B? Neste item, temos as seguintes impedâncias:
Inicialmente, vamos desligar a fonte . Com isso, as impedâncias e ficam em série e a associação destas fica em paralelo com .Olha lá:
Note que temos um divisor de tensão entre e . A tensão em será dada por:
Pela Lei de Ohm, temos que:
Vamos partir para nossa segunda análise, desligando a fonte . Neste caso, teremos a seguinte associação de impedâncias:
Note que temos um divisor de corrente entre e . A corrente em é dada por:
Ou seja, esta corrente passa pela impedância e depois se divide entre as impedâncias e , que caracterizam um divisor de corrente. A corrente em é dada por:
Podemos finalmente somar o resultado das duas análises. Observe que devemos inverter o sinal de para respeitar o sentido da corrente, beleza?
Resposta
a.
b.