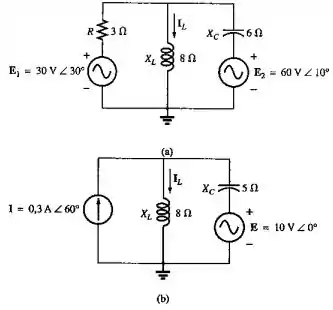
Usando o teorema da superposição, determine a corrente na indutância para os circuitos mostrados na figura 18.109.
Passo 1
E aí, pessoal! De boa? Prontos para mais uma questão?
Vamos começar pela letra A. Antes de tudo, note que teremos as seguintes impedâncias:
Para aplicar o teorema da superposição, primeiro vamos desligar , obtendo um curto circuito no lugar. Nesse caso, veja que e ficarão em paralelo! Vamos as contas:
Prontinho! Agora veja que e estão em série. Logo, a corrente que passa por eles é a mesma! Pela Lei de Ohm, vamos ter:
Para descobrir , teremos que calcular o divisor de corrente entre e . Bora lá!
Passo 2
Agora temos que ligar a fonte e desligar a fonte , obtendo um curto circuito no lugar, e repetir a análise. Nesse caso, e estão em paralelo e esta associação está em série com . Novamente vamos usar a lei de Ohm e em seguida um divisor de corrente. Teremos:
Somando os resultados da primeira e da segunda análise, teremos:
Passo 3
Prontos para letra B? Vamos listar as impedâncias deste circuito:
Show! Agora podemos partir para o teorema da superposição. Vamos começar desligando a fonte , de modo a obter um curto circuito no lugar. Reparem que a fonte de corrente está fornecendo uma corrente ao circuito que se divide entre as duas impedâncias. Então de cara vemos que basta resolver um divisor de corrente! Moleza, né?
Passo 4
Em seguida, devemos ligar a fonte e desligar a fonte , de modo a obter um circuito aberto no lugar. Logo, para descobrir , devemos apenas usar a Lei de Ohm, já que as impedâncias ficam em série!
Somando os resultados da primeira e da segunda análise, teremos:
Resposta
a.
b