Usando o teorema da superposição, determine a expressão senoidal para a corrente i no circuito visto na Figura 18.111.
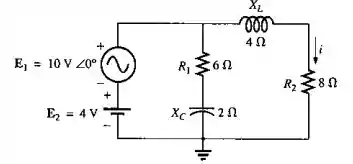
Passo 1
E aí, pessoal! Prontos para mais uma questão de circuitos?
Vamos começar identificando as impedâncias do circuito:
Podemos então aplicar o teorema da superposição. Observe que temos apenas fontes de tensão no circuito, logo, ao desligá-las, devemos substituí-las por um curto circuito.
Passo 2
Em nossa análise inicial, vamos desligar a fonte . Note que teremos apenas a ação de uma fonte de tensão DC. Logo, o capacitor se comporta como circuito aberto e o indutor como um curto circuito.
Como e estão em paralelo com , a tensão nesses resistores é de . Pela lei de Ohm, a corrente em é dada por:
Passo 3
Em seguida, vamos desligar a fonte . A análise é parecida com a anterior. Neste caso, as impedâncias e que estão em paralelo e podemos calcular a corrente em utilizando novamente a lei de Ohm:
Com isso, já conseguimos determinar a expressão senoidal para a corrente :