Use a equação representativa e transformadas de Laplace para calcular , para , se
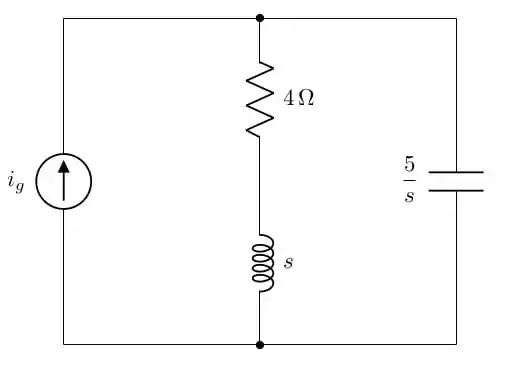
Passo 1
E aí, moçada. Vamos começar nossa jornada resolvendo circuitos usando transformadas ao invés de equações características.
Como o circuito não está chaveado e não foram dadas condições iniciais, tudo o que temos que fazer com o circuito é colocá-lo no domínio da frequência:
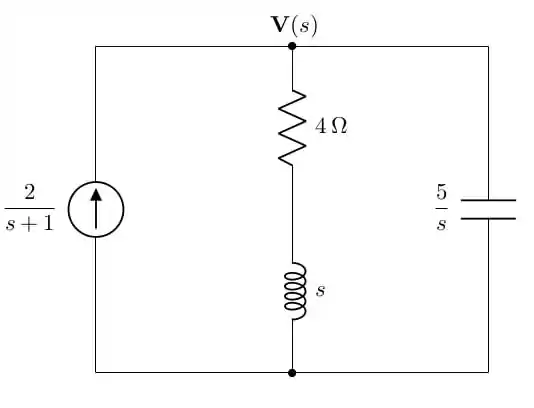
Passo 2
Fazendo a análise de nós do circuito transformado, temos:
Passo 3
Calculando os coeficientes, temos:
Para encontrarmos os coeficientes e , vamos fazer um algebrismo, usando o fato de que já sabemos o valor de .
Como os denominadores são iguais, vamos trabalhar apenas com os numeradores:
Esta última equação nos leva ao seguinte sistema:
As soluções podem ser obtidas de apenas 2 equações. A terceira equação servirá como viés de confirmação para sabermos se os nossos coeficientes estão corretos. Assim:
Assim,
Assim,
Ufa! Conseguimos. Vamos pra próxima?