Use a equação representativa e transformadas de Laplace para calcular , para , se o circuito está em regime permanente em .
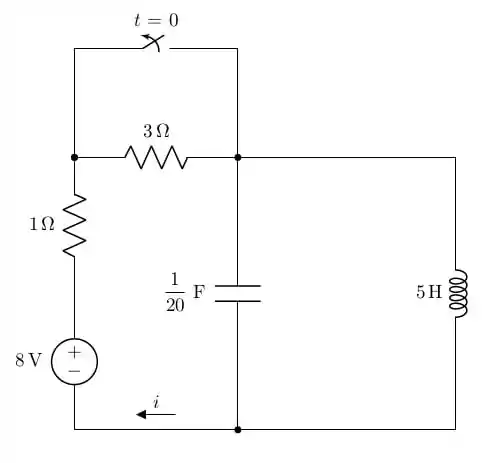
Passo 1
E aí, moçada. Vamos dar continuidade na nossa jornada resolvendo circuitos usando transformadas ao invés de equações características.
O circuito está chaveado e antes do chaveamento o circuito já está em regime permanente. Isso significa que teremos que encontrar a corrente no capacitor e a tensão no indutor. Para o regime permanente em , teremos a seguinte situação:
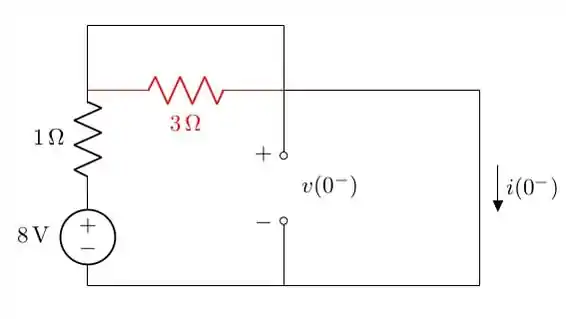
Se observarmos bem, o resistor de está em vermelho porque nesta configuração ele está curto-circuitado, ou seja, é como se ele não existisse. O que sobra é apenas a fonte e o resistor de . Logo
Para calcular , vamos usar a LKT na primeira malha:
Assim, essas são nossas condições iniciais.
Passo 2
De posse das condições iniciais, podemos desenhar o circuito no domínio da frequência com as fontes de tensão associadas a cada condição. No nosso caso, só teremos uma fonte de tensão em série com o indutor.
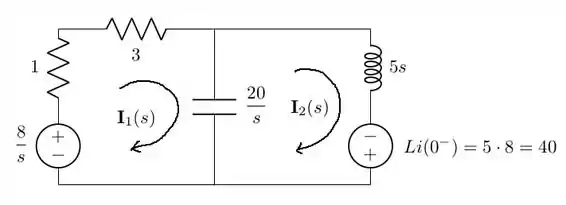
Fazendo uso da análise de malhas, obtemos:
Malha 1:
Reorganizando:
Malha 2:
Reorganizando:
Assim, o nosso sistema é composto das seguintes equações:
Passo 3
Como nosso objetivo é encontrar que coincide com no domínio da frequência, vamos calcular apenas para poupar esforços. Vamos usar o método da adição nesse sistema para eliminar .
Perceba que os termos com são opostos, ou seja, a sua soma vale zero. Assim, ficamos apenas com os demais termos:
Passo 4
Para uma questão tão grande, até que o autor foi bonzinho conosco nos dando apenas polos simples para calcularmos. Isso é feito facilmente usando o método dos resíduos:
Assim,
Logo,
Show de bola! Agora vamos pra próxima!