(a) Verifique se os resultados dos exercícios 2.4 e 2.5 e do Problema 2.11 são coerentes com a Equação 2.33.
(b) Use a lei de Gauss para encontrar o campo dentro e fora de um tubo cilíndrico oco longo, com uma densidade superficial de carga uniforme . Verifique se o resultado é coerente com a Equação 2.33.
(c) Verifique se o resultado do Exemplo 2.7 é coerente com as condições de contorno 2.34 e 2.36.
Passo 1
Faaaala meu povo!! Como vocês estão? Bora lá resolver mais uma questãozinha?
Iniciando o enunciado (a), vamos verificar o exercício 2.4:
Calculando a diferença de potencial:
, confere com o exercício!
Passo 2
Agora verificaremos o exercício 2.5:
Em cada superfície, em um lado e no outro, então o , também confere com o exercício!
Passo 3
Para fecharmos o (a), falaremos do problema 2.11:
A tensão fora é:
A tensão dentro é:
Então:
, também confere com o exercício!
Passo 4
Iniciaremos a (b) com uma figura que exemplifica o nosso cálculo:
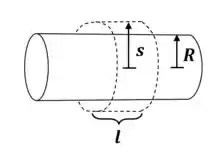
Fora do cilindro:
(na superfície)
Passo 5
Agora dentro do cilindro:
então
Portanto, a diferença de potencial é:
, conforme o exercício 2.11.
Passo 6
Ufa, até que enfim falaremos do enunciado (c).
A tensão fora do cilindro é:
A tensão dentro do cilindro é:
Então:
, confere com o exemplo.
Passo 7
A última condição de contorno que verificaremos é:
Então:
Também confere com o exercício exemplo.
Prontinho, pessoal!! Bora resolver mais uma questão juntos?
Resposta
(a) Todos conferem com os exercícios.
(b) , confere com o 2.11.
(c) conferem com o exemplo.