Verifique o teorema de Stokes para a função usando a área triangular sombreada da figura 1.34.
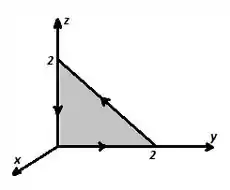
Passo 1
Vamos lá. Temos a seguinte função:
De acordo com o teorema de Stokes, temos:
Então, temos que:
Considerando a volta no sentido anti-horário, teremos:
Então:
Passo 2
Para a integral de linha, vamos considerar três segmentos:
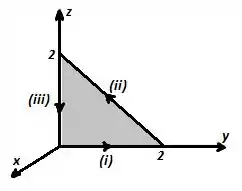
Para :
Para :
Para :
Então, somando o resultado das três integrais temos:
Resposta
Assim verificamos então o teorema de Stokes para a função usando a área dada.
Ficou claro? Espero que sim! xD