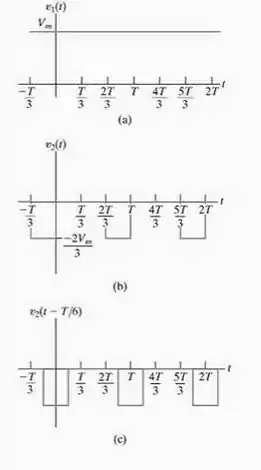
Às vezes, é possível usar simetrias para determinar os coeficientes de Fourier, ainda que a função original não seja simétrica! Com isso em mente, considere a função do Problema para Avaliação 16.1. Observe que pode ser dividida nas duas funções da Figura P16.17(a) e (b). Além do mais, podemos transformar em uma função par deslocando-a T/6 unidades para a direita, o que é mostrado na Figura P16.17(c). Nesse ponto, observamos que e que a série de Fourier de é uma série de um único termo, . Para determinar a série de Fourier de , em primeiro lugar, determinamos a série de Fourier de e, então, deslocamos essa série T/6 unidades para a esquerda. Use a técnica que acabamos de descrever para verificar a série de Fourier dada como resposta ao Problema para Avaliação 16.2(e).
Passo 1
Deixe
and uma vez é par
Portanto
e Por isso, . Simplificando,
Passo 2
Se
Todos os coeficiente são verificados
Resposta
Todos os coeficiente são verificados