Se um corpo não contém planos de simetria, os principais momentos de inércia podem ser determinados matematicamente. Para mostrar como isso é feito, considere o corpo rígido que está girando com velocidade angular ω, direcionado ao longo de um de seus principais eixos de inércia. Se o momento de inércia principal em torno deste eixo é I, o momento angular pode ser expresso como Os componentes de H também podem ser expressos pelas Eqs. 21-10, onde se assume que o tensor de inércia é conhecido. Equacione os componentes i,j ek de ambas as expressões para H e considere , e como desconhecidos. A solução destas três equações é obtida desde que o determinante dos coeficientes seja zero. Mostre que esse determinante, quando expandido, produz a equação cúbica.
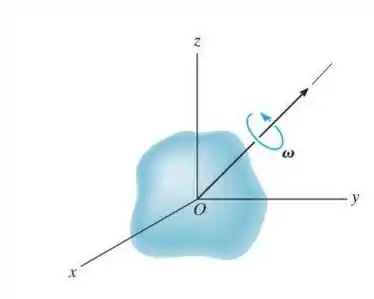
As três raízes positivas de I, obtidas a partir da solução desta equação, representam os principais momentos de inércia , e
Passo 1
O enunciado gurizada pede que a gente determine dos coeficientes seja zero. Mostre que esse determinante, quando expandido, produz a equação cúbica.
Equacionar os componentes i,j,k às equações escalares (Eq. 21-10) produz
Passo 2
Solução para , requer
Expandindo