Torção Mecânica

Fala aí! Procurando um conteúdo ótimo para estudar Torção? Sua busca acabou, vem comigo que vou te ajudar nesse estudo!

Dá uma olhada nessa imagem aqui:

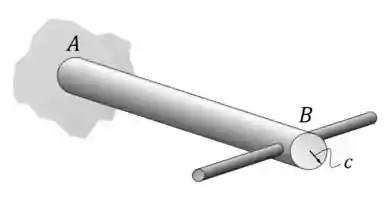
Temos uma barra de raio e, no ponto dessa barra tem duas hastes laterais.

Podemos aplicar um torque nessa barra, aplicando forças nas extremidades das hastes que se encontram no ponto como mostra a figura:

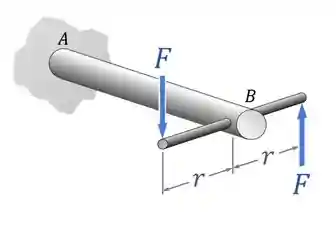
Se fizermos um somatório das forças na vertical temos uma resultante zero, mas cada uma dessas forças gera no eixo principal um torque, de modo que temos um torque resultante no ponto do eixo:

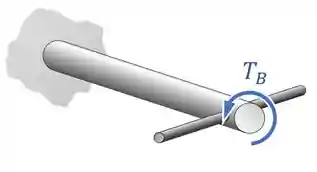
Tá, beleza, aplicamos um torque, mas o que esse torque gera no nosso eixo?

É aí que temos a nossa torção. A torção nada mais é que a tensão gerada em uma barra retilínea em resposta ao torque aplicado que tende a produzir rotação sobre o eixo longitudinal da barra.

Mas vamos com calma para gente entender melhor isso aí.

A primeira coisa que esse torque aplicado externamente vai gerar no nosso eixo é um torque interno igual ao torque externo, mas ao longo de todo o eixo:

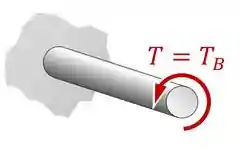
Então, a medida que a peça é carregada com um torque externo, um torque interno é gerado e a peça será deformada:

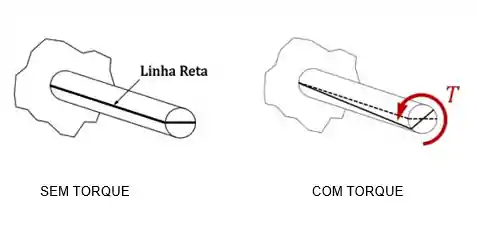
Note que essa deformação acontece nas faces da seção transversal da peça, então estamos diante de uma tensão e deformação cisalhantes.

A torção é definida como essa tensão cisalhante que resulta da aplicação do torque na barra e o representamos pela letra grega "tau", .

Se pensarmos em como essa tensão cisalhante é distribuida ao longo da seção transversal, vemos que ela cresce a medida que nos afastamos do centro:

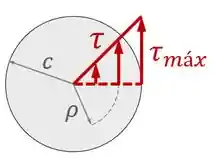
A partir daí podemos expressão uma fórmula para a torção:

Onde:

• é a torção;
• é o torque interno no eixo. Alguns autores o chamam de momento torsor;
• é a distância do centro ao ponto que está sendo estudado, e;
• é o "momento polar de inécia" da seção transversal do eixo

Esse momento polar de inércia é dado pela seguinte fórmula:

Essa é a nossa querida torção.

Olha aqui esse resumo com a fórmulas da torção para facilitar pra você:

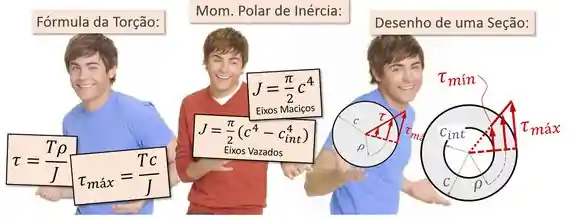
Curtiu? Esse é só o início sobre torção. Temos muito mais conteúdos para complementar e você arrasar na prova. Então, continua aqui com a gente, dá uma navegada pelo nosso Raio-X, logo aqui em seguida, e veja todo esse conteúdo que temos para te oferecer de maneira bem descontraída e didática. 👇🏽 👇🏽