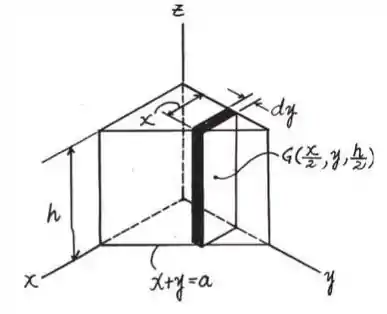
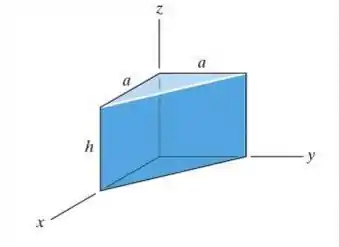
Determine por integração direta o produto da inércia para o prisma homogêneo. A densidade do material é ρ. Expresse o resultado em termos da massa total m do prisma.
Passo 1
O enunciado gurizada pede que a gente determine por integração direta o produto da inércia para o prisma homogêneo. A densidade do material é ρ. Expresse o resultado em termos da massa total m do prisma.
A massa diferencial do elemento é
Usando o teorema dos eixos paralelos: