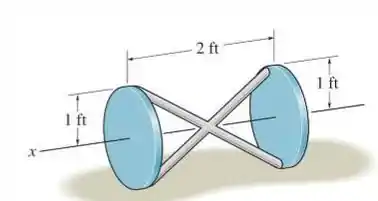
Determine o momento de inércia do conjunto haste e disco em relação ao eixo x. Cada um dos discos tem um peso de 12 libras. As duas hastes pesam 4 libras cada uma e suas extremidades se estendem até as bordas dos discos
Passo 1
O enunciado gurizada pede que a gente determine o momento de inércia do conjunto haste e disco em relação ao eixo x. Cada um dos discos tem um peso de 12 libras. As duas hastes pesam 4 libras cada uma e suas extremidades se estendem até as bordas dos discos
Para uma haste
slug
Passo 2
Para um disco
Por isso