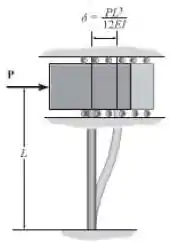
Na ‘teoria da massa em bloco’, um prédio de um só andar pode ser modelado de tal maneira que a massa inteira do prédio é concentrada em seu topo, o qual é apoiado por uma coluna cantiléver de massa desprezível, como mostrado. Quando uma força horizontal é aplicada ao modelo, a coluna deflete um montante , onde é o comprimento efetivo da coluna, é o módulo de elasticidade de Young para o material, e é o momento de inércia da seção transversal da coluna. Se a massa em bloco é , determine a frequência de vibração em termos desses parâmetros.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Por definição, temos que:
Aplicando ao problema, temos:
A frequência natural do sistema é dada por:
A frequência natural de vibração, solicitada na questão é dada por: