Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 100
100- Para a estrutura e o carregamento mostrados na figura, determine a força exercida no elemento em e .
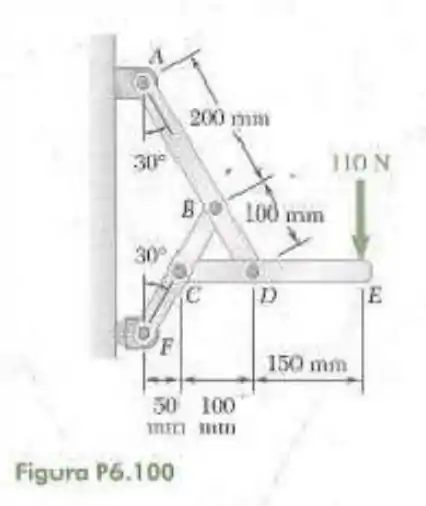
Passo 1
Vamos desenhar as forças de reação na estrutura toda para que possamos tirar as medidas perpendiculares a todas as forças.
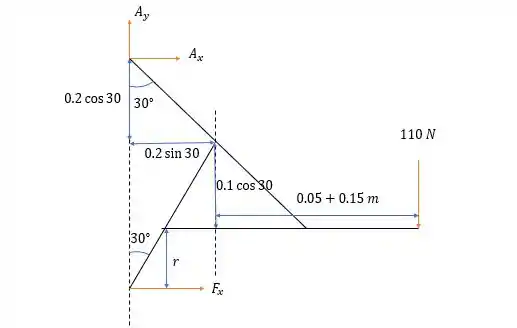
Pela figura o valor de será:
Agora vamos fazer a somatória dos momentos em .
Agora pela somatória das forças horizontais temos que:
E pela somatória das forças verticais:
Passo 2
Agora analisar as forças no elemento e vermos o que tem.
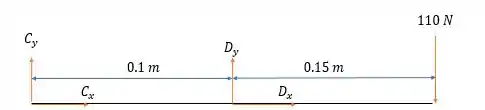
Fazendo a somatória dos momentos em temos:
Sinal negativo, sentido para baixo.
E pela somatória das forças verticais temos:
Sentido para cima
Para encontrar vamos analisar a barra .
Fazendo a somatória dos momentos em .
Como sabemos o valor de e de nós temos:
Como não tem mudança de sinal e na barra ela está apontada para a direita então é esse o sentido real dessa força.
Voltando para a barra vemos que pela somatória das forças horizontais temos:
Logo:
E terá sentido para a esquerda.