Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 10.Problemas - Ex. 12
10.12 Determine o momento de inércia da área em relação ao eixo .
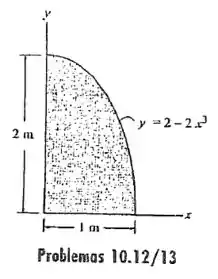
Passo 1
A fórmula do momento de inércia em relação ao eixo é
Nós precisamos escolher um elemento infinitesimal de área que seja paralelo ao eixo :
O elemento infinitesimal de área vai ser igual a
Isolando na função dada:
Então
E os limites de integraçãoo vão ir de 0 até 2, porque vamos integrar em .
Passo 2
Agora é só reolver a integral
Vamos tirar a constante para fora da integral
Vamos usar a técnica de substituição
Os limites de integração vão ser:
Quando :
E quando :
Como a integral não pode ir de 2 até 0, devemos mudar o sinal da integral e inverter os limites de integração:
O menos de fora da integral com o que tem ali dentro de lado do se cancelam:
Quando a gente multiplica o mesmo número com expoentes diferentes, devemos somar os expoentes:
Agora é só fazer a integração do polinômio: